---

| Next || Previous || Top |

SOLUTION_SPECIES

This keyword data block is used to define chemical reaction, log K , and activity-coefficient parameters for each aqueous species. In addition, parameters may be defined for each species that are used to calculate specific conductance, multicomponent diffusion, density, and enrichment in the diffuse layer of surfaces. Normally, this data block is included in the database file and only additions and modifications are included in the input file.

Example data block

Line 0: SOLUTION_SPECIES 
Line 1: CO3-2 + H+ = HCO3-
Line 2: log_k 10.329
Line 3: delta_h -3.561 kcal
Line 4: -analytic 107.8871 0.03252849 -5151.79 -38.92561 563713.9
Line 5: -gamma 5.4000 0.0000
Line 6: -dw 1.18e-9
Line 7: -Vm 8.615 0 -12.21 0 1.667 0 0 264 0 1
Line 7:-Vm 10.26 -2.92 -12.58 -0.241 2.23 0 -5.49 320 2.83e-2 1.144 
Line 8: -Millero 21.07 0.185 -0.002248 2.29 \ -0.006644 -3.667e-06
Line 1a: H2O = OH- + H+
Line 4a: -a_e -283.971 -0.05069842 13323.0 102.24447 -1119669.0
Line 4a:-a_e 293.29227 0.1360833 -10576.913 -123.73158 0 -6.996455e-5
Line 5a: -gamma 3.5000 0.0000
Line 1b: D2O = D2O
Line 2a: log_k 0
Line 9: -activity_water
Line 1c: OH- + HDO = OD- + H2O
Line 2b: log_k -0.301029995663
Line 10: -add_logk Log_alpha_D_OH-/H2O(l)  1.0
Line 5b: -gamma 3.5000 0.0000
Line 1d: Cl- = Cl- 
Line 2c: log_k 0
Line 11: -llnl_gamma 3.0000 
Line 1e: 2H2O = O2 + 4H+ + 4e- 
Line 2d: log_k -85.9951
Line 12: -co2_llnl_gamma
Line 1f: Cs+ = Cs+
Line 2d: log_k 0
Line 13: -erm_ddl 2.1
Line 1g: HS- = S2-2 + H+
Line 2e: log_k -14.528
Line 14: -no_check 
Line 15: -mole_balance S(-2)2
Line 1h: H+ = H+
Line 5b: -gamma 9.0 0
Line 16:     -viscosity 9.35e-2 -8.31e-2 2.487e-2 4.49e-4 
2.01e-2 1.570 
Line 6a:  -dw 9.31e-9 838 16.315 0 2.376 24.01 0
 

Explanation

Line 0: SOLUTION_SPECIES

Keyword for the data block. No other data are input on the keyword line.

Line 1: Association reaction

Association reaction for aqueous species. The defined species must be the first species to the right of the equal sign. The association reaction must precede any identifiers related to the aqueous species. The association reaction is an identity reaction for each primary master species.

Line 2: log_k log K

log_k --Identifier for log K at 25 °C. Optionally, -log_k , logk , -l [ og_k ], or -l [ ogk ].

log K --Log K at 25 °C for the reaction. Log K must be 0.0 for primary master species. Default is 0.0.

Line 3: delta_h enthalpy, [ units ]

delta_h --Identifier for enthalpy of reaction at 25 °C. Optionally, -delta_h , deltah , -d [ elta_h ], or -d [ eltah ].

enthalpy --Enthalpy of reaction at 25 °C for the reaction. Default is 0.0 kJ/mol.

units --Default units are kilojoules per mole. Units may be calories, kilocalories, joules, or kilojoules per mole. Only the energy unit is needed (per mole is assumed) and abbreviations of these units are acceptable. Default units are kJ/mol. Explicit definition of units for all enthalpy values is recommended. The enthalpy of reaction is used in the Van’t Hoff equation to determine the temperature dependence of the equilibrium constant. Internally, all enthalpy calculations are performed with the units kJ/mol.

Line 4: -analytic A ₁ , A ₂ , A ₃ , A ₄ , A ₅ , A ₆

-analytic --Identifier for coefficients for an analytical expression for the temperature dependence of log K . Optionally, analytical_expression , a_e , ae , -a [ nalytical_expression ], -a [ _e ], -a [ e ].

A ₁ , A ₂ , A ₃ , A ₄ , A ₅ , A ₆ --Six values defining log K as a function of temperature in the expression 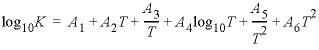, where T is in kelvin.

Line 5: -gamma Debye-Hückel a, Debye-Hückel b

-gamma --Indicates activity-coefficient parameters are to be entered. If -gamma is entered, then the equation from WATEQ (Truesdell and Jones, 1974) is used, 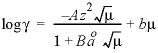. In this equations, is the activity coefficient, is ionic strength, and A and B are constants at a given temperature. If -gamma is not input for a species, then for a charged species the Davies equation is used to calculate the activity coefficient:

; for an uncharged species the following equation is used: . Optionally, -g [ amma ].

Debye-Hückel a --Ion-size parameter in the WATEQ activity-coefficient equation.

Debye-Hückel b --Parameter b in the WATEQ activity-coefficient equation.

Line 6: -dw Dw(25C) dw_T a a2 visc a3 a_v_dif

-dw --Identifier for tracer diffusion coefficient of the species. Tracer diffusion coefficients are used in the multicomponent diffusion calculation in TRANSPORT and in calculating the specific conductance of a solution (Basic function SC). Default is 0 m ² /s (square meter per second) if -dw is not included. Optionally, dw or -dw .

Dw(25C)—Tracer diffusion coefficient for the species at 25 °C, m ² /s.

dw_T—Temperature dependence for diffusion coefficient.

a— Debye-Huckel ion size for correcting the ionic strength dependent contribution of the species to the specific conductance (SC).

a2— Exponent for the volume correction of a in the SC calculation.

Visc— Exponent for the viscosity correction in the SC calculation.

a3— Ionic strength exponent, or a flag (see Notes).

A_v_dif— Exponent for (viscosity_0_tc/viscosity), for correcting the tracer diffusion coefficient in TRANSPORT calculations.

Line 6: -dw diffusion coefficient damp a1 a2

-dw --Identifier for tracer diffusion coefficient. Tracer diffusion coefficients are used in the multicomponent diffusion calculation in TRANSPORT and in calculating the specific conductance of a solution (Basic function SC). Default is 0 m ² /s (square meter per second) if -dw is not included. Optionally, dw or -dw .

diffusion coefficient—Tracer diffusion coefficient for the species at 25 °C, m ² /s.

damp --Damping parameter for the temperature effect on viscosity on the diffusion coefficient. Dw(TK) = D * exp(damp / TK - damp / 298.15) * TK * 0.89 / (298.15 * viscos), where Dw is the diffusion coefficient at temperature TK kelvin; D is the diffusion coefficient defined by the first parameter; damp is the damping factor; and viscos is the viscosity of the solution.

a1 --Parameter for the ionic strength effects on the diffusion coefficient of ions in electro-migration. Dw(I) = Dw(TK) * exp(a1 * DH_A * |z| * I^0.5 / (1 + DH_B * I^0.5 * a2 / (1 + I^0.75))), where Dw(I) is the diffusion coefficient corrected for temperature and ionic strength; Dw(TK) is the diffusion coefficient corrected for temperature; a1 is the third parameter defined in -dw; DH_A is the Debye-Huckel A parameter; z is the absolute value of the charge of the aqueous species; I is the ionic strength; DH_B is the Debye-Huckel B parameter; and a2 is the fourth parameter defined in -dw.

a2--Parameter for the ionic strength effects on the diffusion coefficient of ions in electro-migration in the equation above.

Line 7: -Vm a1, a2, a3, a4, W, i1, i2, i3, i4

-Vm --Identifier for parameters used to calculate the specific volume (cm ³ /mol) of aqueous species with a Redlich-type equation (see Redlich and Meyer, 1964). As explained in the following Notes section, the volume of species i is calculated, by convention relative to the reference volume of H ⁺ of 0, as , where the first term of the right-hand side, , is the specific volume at infinite dilution, and the second and third terms are functions of the ionic strength and the ion-size parameter in the extended Debye-Hückel equation, and i1, i2, i3 and i4.

The specific volume at infinite dilution is parameterized with SUPCRT92 formulas (Johnson and others, 1992):

,

where 41.84 transforms cal mol ^-1 bar ^-1 (calorie per mole per bar) into cm ³ /mol, P _b is pressure in bar, T _K is temperature in kelvin, W x Q _Born is the Born volume, calculated from W and the pressure dependence of the dielectric constant of water.

The second term contains A _{v ,} the Debye-Hückel limiting slope, which is calculated as a function of temperature and pressure, and the extended Debye-Hückel equation (see the Notes).

The coefficient is calculated as .

a1, a2, a3, a4, W, i1, i2, i3, i4 --Numerical values for parameters a1 to a4 (cal mol ^-1 bar ^-1 , cal/mol (calorie per mole), cal K mol ^-1 bar ^-1 [calorie kelvin per mole per bar), cal K mol ^-1 [calorie kelvin per mol], respectively), the Born coefficient W (cal/mol), the Debye-Hückel ^{ion-size parameter} (10-10 m), and i1 (cm ³ /mol), i2 (cm ³ K mol ^-1 ), i2 (cm ³ K ^-1 mol ^-1 ) and i4 (-), used in the equation for calculating the conventional specific volume of a solute species.

Line 8: -Millero a, b, c, d, e, f

-Millero --Alternative formulation for calculating the specific volume for the aqueous species (Millero, 2000) by convention relative to the volume of H ⁺ of 0 at ionic strength of 0. The specific volume for species i is calculated according to the formula , where is the specific volume at infinite dilution; A _v is the Debye-Hückel limiting slope, and I is the ionic strength. The volume at infinite dilution is parameterized as and the coefficient is parameterized as , where T is °C. If both - Vm and - Millero are defined for a species, the numbers from - Vm are used. Warning: the applicability of the Millero formulas is limited to T < 50 °C, and the calculated densities may be incorrect at ionic strengths > 1.0 except for NaCl solutions. Optionally, Millero or -Mi [ llero ].

a, b, c, d, e, f --Numerical values for parameters a to f in the specific volume equation.

Line 9: -activity_water

-activity_water --Identifier indicates that the species is an isotopic form of water. The activity coefficient for the species is such that its activity is equal to mole fraction in solution. Optionally, activity_water or -ac [ tivity_water ].

Line 10: -add_logk named log K, coefficient

-add_logk --Identifier defining an additional term for the equilibrium constant of the species. The identifier is used primarily in defining the equilibrium constant for isotopic species that require the addition of an isotopic fractionation factor. Optionally, add_logk , add_log_k , -ad [ d_logk ] or -ad [ d_log_k ].

named log K --Name of an expression defined in a MIX_EQUILIBRIUM_PHASES data block.

coefficient --Coefficient for the expression named log K ; the value of the expression is multiplied by coefficient and added to the log K for the species.

Line 11: -llnl_gamma diameter

-llnl_gamma --Identifier for the hard-core diameter in the expression for the activity coefficient in the Lawrence Livermore aqueous model; this identifier can be used only with the Lawrence Livermore National Laboratory aqueous model ( llnl.dat ). Optionally, llnl_gamma or -ll [ nl_gamma ].

diameter --Hard-core diameter for the species.

Line 12: -co2_llnl_gamma

-co2_llnl_gamma --The activity coefficient for carbon dioxide is used as the activity coefficient for this uncharged species; this identifier can be used only with the Lawrence Livermore National Laboratory aqueous model ( llnl.dat ). Optionally, co2_llnl_gamma or -co [ 2_llnl_gamma ].

Line 13: -erm_ddl factor

-erm_ddl --Identifier for the enrichment factor for a species in the diffuse double layer of surfaces calculated with the -Donnan identifier in the SURFACE data block. Optionally, erm_ddl or -e [ rm_ddl ].

factor --Enrichment factor. Default is 1.0 (unitless).

Line 14: -no_check

-no_check --Indicates the reaction equation should not be checked for charge and elemental balance. Generally, equations should be checked for charge and elemental balance. The only exceptions might be polysulfide species that assume equilibrium with a solid phase; this assumption has the effect of removing solid sulfur from the mass-action equation. By default, all equations are checked. However, the identifier -mole_balance is needed to ensure that the proper number of atoms of each element are included in mole-balance equations (see -mole_balance ). Optionally, no_check or -n [ o_check ].

Line 15: -mole_balance formula

-mole_balance --Indicates the stoichiometry of the species will be defined explicitly. Optionally, mole_balance , mass_balance , mb , -m [ ole_balance ], -mass_balance , or -m [ b ].

formula --Chemical formula defining the stoichiometry of the species. Normally, both the stoichiometry and mass-action expression for the species are determined from the chemical equation that defines the species. Rarely, it may be necessary to define the stoichiometry of the species separately from the mass-action equation. The polysulfide species provide an example. These species are usually assumed to be in equilibrium with native sulfur. The activity of a pure solid is 1.0, and thus the term for native sulfur does not appear in the mass-action expression (Line 1g). The S ₂ ^- species contains two atoms of sulfur, but the chemical equation indicates it is formed from species containing a total of one sulfur atom. The -mole_balance identifier is needed to give the correct stoichiometry. Note that unlike all other chemical formulas used in PHREEQC, the valence state of the element can and should be included in the formula of Line 15. The example indicates that the polysulfide species will be summed into the S(-2) mole-balance equation.

Line 16: -viscosity b0, b1, b2, d1, d2, d3, tan

- viscosity --Defines viscosity parameters for the species. Optionally, viscosity or -vi[scosity].

b0, b1, b2, d1, d2, d3, tan—See explanation in the following Notes section for the equations and parameters used for viscosity.

Notes

Line 1 must be entered first in the definition of a species. Additional sets of lines (Lines 1-7 as needed) may be added to define all of the aqueous species. A log K should be defined for each species with either log_k (Line 2) or -analytical_expression (Line 4); the default of 0.0 is not meaningful for most association reactions. In this Example data block, the following types of aqueous species are defined: (a) a primary master species, SO ₄ ^{-2 ,} for which the reaction is an identity reaction and log K is 0.0; (b) a secondary master species, HS ^- , for which the reaction contains electrons; (c) an aqueous species that is not a master species, OH ^- ; and (d) an aqueous species for which the chemical equation does not balance, S ₂ ^-2 . If an activity coefficient of 1 is needed for a species, use -gamma 1e5 0 in Line 5.

The tracer diffusion coefficient is for a trace concentration of the solute species in pure water. Usually, it is determined by measuring the specific conductance of solutions at various concentrations and extrapolating to zero concentration (Robinson and Stokes, 2002). The molar conductivity of a solute species and its diffusion coefficient are related by , where is the molar conductivity (S/m / (mol/m3) equals S m ² mol ^-1 ) (siemens square meter per mole), zi is the charge number (unitless) of species i, F is Faraday's constant (C/mol, coulomb per mole), R is the gas constant (J K-1mol-1, joule per kelvin per mole), T is the absolute temperature (K), and Dw, i is the diffusion coefficient (m2/s). PHREEQC calculates the specific conductance of a solution by summing the product of the specific conductivity and the molal concentration of all the species in solution, while correcting the molal concentration with an electrochemical activity coefficient that is derived from a combination of Kohlrausch’s law and the Debye-Hückel equation as explained in http://www.hydrochemistry.eu/exmpls/sc.html (accessed June 25, 2012). The tracer diffusion coefficient is corrected for the temperature T (K) of the solution by D ^’ _w,i = (D _w,i )298 × × , where η is the viscosity of water (Atkins and de Paula, 2002). The tracer diffusion coefficient is corrected for the temperature T(K) of the solution by Dw(TK) = Dw(298) * exp(dw_T / TK - dw_T / 298.15) * viscos_0_25 / viscos_0_tc, where viscos_0_25 and viscos_0_tc are the viscosities of water at 25 and tc (the temperature of the solution, oC), respectively, calculated with the polynomials of Huber et al., 2009, J. Phys. Chem. Ref. Data, Vol. 38, 101-125. Optionally, for TRANSPORT calculations, the diffusion coefficient can be corrected for the viscosity of the solution with the a_v_dif parameter: Dw(TK) = Dw(TK) * (viscos_0_tc / viscos)^a_v_dif, where viscos is the T,P,I-dependent viscosity of the solution.

The specific conductance is calculated with a corrected Dw(TK), using the parameters defined in line 6a:

Dw(TK) = Dw(TK) * viscos_0_tc / viscos)^visc (visc = 2.376 for H+ in line 6a)

If a3 > 5 or a3 = 0 or not defined, then the Debye-Hückel ka = DH_B * a * (1 + (vm - v0))^a2 * mu^0.5 (DH_B is the Debye-Hückel B parameter, a = 16.315 for H+, vm = is the T,P,I dependent volume of the ion, v0 is the T,P dependent volume at I = 0, a2 = 0 for H+, the reference for the molar volume of the ions, with vm = vo = 0)

If a3 = -10, then ka = DH_B * a * mu^a2 (Define a3 = -10, not used in this database.) (a3 = 24.01 for H+, a flag to indicate the use of the Debye-Huckel-Onsager-Falkenhagen formulas.)

If -3 < a3 < 4, then ka = DH_B * a2 * mu^0.5 / (1 + mu^a3), Appelo, 2017, Cement and Concrete Research, 101, 102-113. And Dw(I) = Dw(TK) * exp(-a * DH_A * z * sqrt_mu / (1 + ka)) (used for Sr+2 in PHREEQC.DAT).

The Dw and a_v_dif can be set in a USER_ program with setdiff_c("name", Dw, a_v_dif), for example: 10 print setdiff_c("H+", 9.31e-9, 1).

If -Vm is defined, the specific volume of species i is calculated, by convention relative to the reference volume of H ⁺ of 0, as

,

where the first term of the right-hand side, , is the volume at infinite dilution; and the second and third terms are functions of the ionic strength .

In the second term, z is the charge number of the species, A _v is the Debye-Hückel limiting slope,

(cm ³ /mol) (mol/kg) ^{-0.5 ,}

with the Debye length factor, 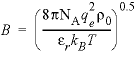(1/cm)(kg/mol) ^0.5 , Avogadro’s number N _A = 6.022 × 10 ²³ molecules per mole, the electron charge q _e = 4.803 × 10 ^-10 esu (electrostatic unit of charge), the density of pure water ñ ₀ (g/cm ³ ), the relative dielectric constant å _r , the Boltzmann constant k _B = 1.38 × 10 ^-16 erg/K (erg per kelvin), the temperature T (K), the pressure P (atm), and the compressibility of pure water ê ₀ (atm ^-1 ). PHREEQC calculates the relative dielectric constant as a function of temperature and pressure, as well as its pressure dependence, according to Bradley and Pitzer (1979), and the density of pure water along the saturation line with equation 2.6 of Wagner and Pruss (2002) and at higher pressures and temperatures with interpolation functions based on IAPWS (International Association for the Properties of Water and Steam) (http://www.nist.gov/srd/upload/NISTIR5078-Tab3.pdf) or with the IF97 (http://www.iapws.org/release.htm) polynomial for region 1 (273 < T < 623 °C, P _sat < P < 100 MPa, megapascal). The Bradley and Pitzer equations also are used to calculate 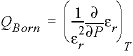, which is a part of . The specific volumes are used to derive the volume changes of reactions, and hence, the pressure dependency of reaction constants for species, and the pressure dependent solubilities of minerals and gases. The volumes also are used for calculating the density of solutions in PHREEQC as implemented by Vincent Post (Free University, Amsterdam, Netherlands, written commun., 2009) based on the work of Millero (2000). The parameters, entered with the identifier -Vm in the phreeqc.dat and pitzer.dat databases and commented with “# supcrt modified”, were obtained by least squares fitting of the specific volumes of salts in aqueous solution, compiled by Laliberté (2009), supplemented with data at lower concentrations (omitted by Laliberté (2009)) and at higher temperatures. In the databases, the ion-size parameter for anions in the extended Debye-Hückel equation, is equal to 0, and for cations equal to the Debye -Hückel a parameter that is entered with -gamma a. The values defined with -Millero in some (now obsolete) databases are, in principle, for the temperature range from 0 to 50 ^o C (Millero, 2000) and may be incorrect for high ionic strengths except for solutions containing predominantly alkali cations and chloride anions.

The Lawrence Livermore National Laboratory aqueous model (Daveler and Wolery, 1992) uses the following expression for the log (base 10) of an activity coefficient: , where , , and are Debye-Hückel parameters that are functions of temperature as defined in the LLNL_AQUEOUS_MODEL_PARAMETERS data block; z _i is the charge number for species i, is the hard-core diameter, which is defined for an aqueous species in the SOLUTION_SPECIES data block with the -llnl_gamma identifier; and I is the ionic strength. The activity for an uncharged species in the Lawrence Livermore National Laboratory aqueous model can be set to a function of temperature by using the -co2_llnl_gamma identifier. The function of temperature is defined by the -co2_coefs identifier in the LLNL_AQUEOUS_MODEL_PARAMETERS data block.

The enrichment factor entered with -erm_ddl multiplies the concentration that is calculated with the Boltzmann equation for the Donnan space on a charged surface. With this factor, the concentrations in the Donnan space are calculated as:

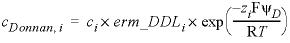, (4)

where cDonnan, i is the concentration of species i in the Donnan pore space (mol/L), ci is the concentration in the free (uncharged) solution, erm_DDLi is an enrichment factor (unitless) that can be defined in keyword SOLUTION_SPECIES, zi is charge number (unitless), F is the Faraday constant (96485 JV-1eq-1, joule per volt per equivalent), ψD is the potential of the Donnan volume (V, volt), R is the gas constant (8.314 JK-1mol-1), and T is the absolute temperature (K). The potential ψD is adapted to let the charge of the Donnan volume counterbalance the surface charge:

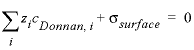, (5)

where σsurface is the surface charge (eq/L, equivalent per liter). The enrichment factor is useful for modeling the relative enrichment or depletion of equally charged species in the electrostatic layer on a charged surface, which is related to enhanced complexation in a low dielectric permittivity medium (Appelo and others, 2010).

By default, equation checking for charge and elemental balance is in force for each equation that is processed. Checking can only be disabled by using -no_check for each equation that is to be excluded from the checking process.

The viscosity of the solution at P, T is now calculated and printed in the output file, and can be retrieved in Basic programs with the function viscos (in previous versions, viscos returned the viscosity of pure water at P, T). The calculation uses a modified Jones-Dole equation which sums the contributions of individual solutes:
η / η₀ = 1 + A √(0.5 ∑ z_im_i) + ∑ f_an (B_im_i + D_im_in_i),
where η is the viscosity of the solution (mPa s), η₀ idem of pure water at the temperature and pressure of the solution, m_i is the molality of species i, made dimensionless by dividing by 1 molal, and z_i is the absolute charge number. A is derived from Debye-Hückel theory, and f_an, B, D and n are coefficients that incorporate volume, ionic strength and temperature effects.
The coefficients are:
B = b₀ + b₁ exp(-b₂ tC)
where b_0..2 are coefficients, and tC is the temperature in ºC. The temperature is limited to 200°C.
f_an = (2 - t_an V_an / V_Cl^-)
for anions, with t_an a coefficient and V_an the P, T and I dependent, apparent volume of the anion relative to the one of Cl^-, which is used as reference species. For cations, f_an = 1 and t_an needs not be defined.
D = d₁ exp(-d₂ tC )
where d_{1, 2} are coefficients.
n = ((1 + f_I)^d₃ + ((z_i² + z_i) / 2 · m_i)^d₃ / (2 + f_I)
where f_I averages ionic strength effects and d₃ is a coefficient.
The coefficients are fitted on measured viscosities of binary solutions, for example for H⁺:
SOLUTION_SPECIES
H+ = H+
  -viscosity 9.35e-2 -8.31e-2 2.487e-2 4.49e-4 2.01e-2 1.570    0
  #          b0       b1      b2      d1      d2      d3     tan

Example problems

The keyword SOLUTION_SPECIES is used in example problems 1, 7, 9, 14, 15, and 21 and in all databases.

Related keywords

SOLUTION_MASTER_SPECIES.

---

| Next || Previous || Top |