| Next || Previous || Top |
Example 6--Reaction-Path Calculations
In this example, the precipitation of phases as a result of incongruent dissolution of K-feldspar (microcline) is investigated. Only the four phases originally addressed by Helgeson and others (1969)--K-feldspar, gibbsite, kaolinite, and K-mica (muscovite)--are considered. The thermodynamic data for the phases (table 21, PHASES keyword) are derived from Robie and others (1978) and are the same as for test problem 5 in the PHREEQE manual (Parkhurst and others, 1980).
PHREEQC can be used to solve this problem in three ways: the individual intersections of the reaction path and the phase boundaries on a phase diagram can be calculated (simulation 6A, table 21), the reaction path can be calculated incrementally (simulation 6B, table 21), or the reaction path can be calculated as a kinetic process (simulation 6C, table 21). In the first approach, no knowledge of the amounts of reaction is needed, but a number of simulations are necessary to find the appropriate phase-boundary intersections. In the second approach, only one simulation is sufficient, but the appropriate amounts of reaction must be known beforehand. In the third approach, a kinetic rate expression is used to calculate the reaction path by using a step-size adjusting algorithm, which takes care of phase boundary transitions by automatically decreasing the time interval when necessary. Only the total time to arrive at the point of K-feldspar equilibrium is required. All three approaches are demonstrated here. PHREEQC implicitly contains all the logic of a complete reaction-path program (for example, Helgeson and others, 1970; Wolery, 1979; Wolery and others, 1990). Moreover, the capability to calculate directly the phase boundary intersections provides an efficient way to outline reaction paths on phase diagrams, and the option to add the reaction incrementally and automatically find the stable phase assemblage allows points on the reaction path between phase boundaries to be obtained easily. The kinetic approach and the Basic interpreter that is embedded in PHREEQC can be used to save and print the arrival time and the aqueous composition at each phase transition.
Conceptually, example 6 considers the reactions that would occur if K-feldspar were placed in a beaker and allowed to react slowly. As K-feldspar dissolves, other phases may begin to precipitate. It is assumed that only gibbsite, kaolinite, or K-mica can form, and that these phases will precipitate reversibly if they reach saturation. That is, the phases that precipitated at the beginning of the reaction are allowed to redissolve, if necessary, to maintain equilibrium as the reaction proceeds.
Table 21. Input file for example 6.
TITLE Simulation 6A.--React to phase boundaries.
|
SOLUTION 1 PURE WATER
|
pH 7.0 charge
|
temp 25.0
|
PHASES
|
Gibbsite
|
Al(OH)3 + 3 H+ = Al+3 + 3 H2O
|
log_k 8.049
|
delta_h -22.792 kcal
|
Kaolinite
|
Al2Si2O5(OH)4 + 6 H+ = H2O + 2 H4SiO4 + 2 Al+3
|
log_k 5.708
|
delta_h -35.306 kcal
|
K-mica
|
KAl3Si3O10(OH)2 + 10 H+ = 3 Al+3 + 3 H4SiO4 + K+
|
log_k 12.970
|
delta_h -59.377 kcal
|
K-feldspar
|
KAlSi3O8 + 4 H2O + 4 H+ = Al+3 + 3 H4SiO4 + K+
|
log_k 0.875
|
delta_h -12.467 kcal
|
SELECTED_OUTPUT
|
-file ex6A-B.sel
|
-activities K+ H+ H4SiO4
|
-si Gibbsite Kaolinite K-mica K-feldspar
|
-equilibrium Gibbsite Kaolinite K-mica K-feldspar
|
END
|
TITLE Simulation 6A1.--Find amount of K-feldspar dissolved to
|
reach gibbsite saturation.
|
USE solution 1
|
EQUILIBRIUM_PHASES 1
|
Gibbsite 0.0 KAlSi3O8 10.0
|
Kaolinite 0.0 0.0
|
K-mica 0.0 0.0
|
K-feldspar 0.0 0.0
|
USER_GRAPH 1 Simulation 6
|
-headings 6A--Intersections
|
-chart_title "K-Feldspar Reaction Path"
|
-axis_titles "Log[H4SiO4]" "Log([K+] / [H+])"
|
-axis_scale x_axis -8.0 0.0 1 1
|
-axis_scale y_axis -1.0 8.0 1 1
|
10 PLOT_XY LA("H4SiO4"),(LA("K+")-LA("H+")), color = Red, line_w = 0, \
|
symbol = Circle, symbol_size = 10
|
END
|
TITLE Simulation 6A2.--Find amount of K-feldspar dissolved to
|
reach kaolinite saturation.
|
USE solution 1
|
EQUILIBRIUM_PHASES 1
|
Gibbsite 0.0 0.0
|
Kaolinite 0.0 KAlSi3O8 10.0
|
K-mica 0.0 0.0
|
K-feldspar 0.0 0.0
|
END
|
TITLE Simulation 6A3.--Find amount of K-feldspar dissolved to
|
reach K-mica saturation.
|
USE solution 1
|
EQUILIBRIUM_PHASES 1
|
Gibbsite 0.0 0.0
|
Kaolinite 0.0 0.0
|
K-mica 0.0 KAlSi3O8 10.0
|
K-feldspar 0.0 0.0
|
END
|
TITLE Simulation 6A4.--Find amount of K-feldspar dissolved to
|
reach K-feldspar saturation.
|
USE solution 1
|
EQUILIBRIUM_PHASES 1
|
Gibbsite 0.0 0.0
|
Kaolinite 0.0 0.0
|
K-mica 0.0 0.0
|
K-feldspar 0.0 KAlSi3O8 10.0
|
END
|
TITLE Simulation 6A5.--Find point with kaolinite present,
|
but no gibbsite.
|
USE solution 1
|
EQUILIBRIUM_PHASES 1
|
Gibbsite 0.0 KAlSi3O8 10.0
|
Kaolinite 0.0 1.0
|
END
|
TITLE Simulation 6A6.--Find point with K-mica present,
|
but no kaolinite
|
USE solution 1
|
EQUILIBRIUM_PHASES 1
|
Kaolinite 0.0 KAlSi3O8 10.0
|
K-mica 0.0 1.0
|
END
|
TITLE Simulation 6B.--Path between phase boundaries.
|
USE solution 1
|
EQUILIBRIUM_PHASES 1
|
Kaolinite 0.0 0.0
|
Gibbsite 0.0 0.0
|
K-mica 0.0 0.0
|
K-feldspar 0.0 0.0
|
REACTION 1
|
K-feldspar 1.0
|
0.04 0.08 0.16 0.32 0.64 1.0 2.0 4.0
|
8.0 16.0 32.0 64.0 100 200 umol
|
USER_GRAPH
|
-headings 6B--Increments
|
10 PLOT_XY LA("H4SiO4"),(LA("K+")-LA("H+")), color = Blue, line_w = 0, \
|
symbol = XCross, symbol_size = 7
|
END
|
TITLE Simulation 6C.--kinetic calculation
|
SOLUTION 1
|
-units mol/kgw
|
Al 1.e-13
|
K 1.e-13
|
Si 3.e-13
|
EQUILIBRIUM_PHASES 1
|
Gibbsite 0.0 0.0
|
Kaolinite 0.0 0.0
|
K-mica 0.0 0.0
|
KINETICS 1
|
K-feldspar
|
# k0 * A/V = 1e-16 mol/cm2/s * (10% fsp, 0.1mm cubes) 136/cm = 136.e-13 mol/dm3/s
|
-parms 1.36e-11
|
-m0 2.16
|
-m 1.94
|
-step_divide 1e-6
|
-steps 1e2 1e3 1e4 1e5 1e6 1e7 1e8
|
# -steps 1e2 1e3 1e4 1e5 63240.0 64950.0 1347610.0 1010300.0 45242800.0
|
INCREMENTAL_REACTIONS true
|
RATES
|
K-feldspar
|
-start
|
10 REM store the initial amount of K-feldspar
|
20 IF EXISTS(1) = 0 THEN PUT(M, 1)
|
30 REM calculate moles of reaction
|
40 SR_kfld = SR("K-feldspar")
|
50 moles = PARM(1) * (M/M0)^0.67 * (1 - SR_kfld) * TIME
|
60 REM The following is for printout of phase transitions
|
80 REM Start Gibbsite
|
90 if ABS(SI("Gibbsite")) > 1e-3 THEN GOTO 150
|
100 i = 2
|
110 GOSUB 1500
|
150 REM Start Gibbsite -> Kaolinite
|
160 if ABS(SI("Kaolinite")) > 1e-3 THEN GOTO 200
|
170 i = 3
|
180 GOSUB 1500
|
200 REM End Gibbsite -> Kaolinite
|
210 if ABS(SI("Kaolinite")) > 1e-3 OR EQUI("Gibbsite") > 0 THEN GOTO 250
|
220 i = 4
|
230 GOSUB 1500
|
250 REM Start Kaolinite -> K-mica
|
260 if ABS(SI("K-mica")) > 1e-3 THEN GOTO 300
|
270 i = 5
|
280 GOSUB 1500
|
300 REM End Kaolinite -> K-mica
|
310 if ABS(SI("K-mica")) > 1e-3 OR EQUI("Kaolinite") > 0 THEN GOTO 350
|
320 i = 6
|
330 GOSUB 1500
|
350 REM Start K-mica -> K-feldspar
|
360 if ABS(SI("K-feldspar")) > 1e-3 THEN GOTO 1000
|
370 i = 7
|
380 GOSUB 1500
|
1000 SAVE moles
|
1010 END
|
1500 REM subroutine to store data
|
1510 if GET(i) >= M THEN RETURN
|
1520 PUT(M, i)
|
1530 PUT(TOTAL_TIME, i, 1)
|
1540 PUT(LA("K+")-LA("H+"), i, 2)
|
1550 PUT(LA("H4SiO4"), i, 3)
|
1560 RETURN
|
-end
|
USER_PRINT
|
10 DATA "A: Gibbsite ", "B: Gibbsite -> Kaolinite ", \
|
"C: Gibbsite -> Kaolinite ", "D: Kaolinite -> K-mica ", \
|
"E: Kaolinite -> K-mica ", "F: K-mica -> K-feldspar"
|
20 PRINT \
|
" Transition Time K-feldspar LA(K/H) LA(H4SiO4)"
|
30 PRINT " transfer"
|
40 PRINT " (umoles)"
|
50 FOR i = 2 TO 7
|
60 READ s$
|
70 IF EXISTS(i) THEN PRINT s$, GET(i,1), (GET(1) - GET(i))*1e6, GET(i,2), GET(i,3)
|
80 NEXT i
|
SELECTED_OUTPUT
|
-file ex6C.sel
|
-reset false
|
USER_PUNCH
|
-headings pH+log[K] log[H4SiO4]
|
10 PUNCH LA("K+")-LA("H+") LA("H4SiO4")
|
USER_GRAPH
|
-headings 6C--Kinetics
|
10 PLOT_XY LA("H4SiO4"),(LA("K+")-LA("H+")), color = Blue, line_w = 2, symbol = None
|
END
|
PRINT; -user_print false
|
# --Plot the phase boundaries with USER_GRAPH..
|
PHASES
|
K_H; KH = K+ - H+; -no_check
|
USER_GRAPH
|
-initial_solutions true
|
10 PLOT_XY LA("H4SiO4"), SI("K_H"), color = Black, symbol = None
|
SOLUTION 1
|
pH 11; K 1 K_H 8; Al 1 Gibbsite; Si 1 K-mica
|
SOLUTION 2
|
pH 7; K 1 K-mica; Al 1 Gibbsite; Si 1 Kaolinite
|
SOLUTION 3
|
pH 7; K 1 K-mica; Al 1 K-feldspar; Si 1 Kaolinite
|
SOLUTION 4
|
pH 7; K 1 K_H -1; Al 1 Kaolinite; Si 1 K-feldspar
|
END
|
USER_GRAPH
|
10 PLOT_XY LA("H4SiO4"), SI("K_H"), color = Black, symbol = None
|
SOLUTION 1
|
pH 11; K 1 K_H 8; Al 1 K-feldspar; Si 1 K-mica
|
SOLUTION 2
|
pH 7; K 1 K-mica; Al 1 K-feldspar; Si 1 Kaolinite
|
SOLUTION 3
|
pH 7; K 1 K-mica; Al 1 Gibbsite; Si 1 Kaolinite
|
SOLUTION 4
|
pH 7; K 1 K_H -1; Al 1 Gibbsite; Si 1 Kaolinite
|
END
|
The input file (table 21) first defines pure water with SOLUTION input and the thermodynamic data for the phases with PHASES input. Some of the minerals are defined in the database file (
phreeqc.dat
), but inclusion in the input file replaces any previous definitions for the duration of the run (the database file is not altered). SELECTED_OUTPUT is used to write a file of data that was used to produce table 22, and USER_GRAPH produces the chart shown in figure 7. SELECTED_OUTPUT specifies that the log of the activities of the potassium ion, hydrogen ion, and silicic acid; the saturation indices for gibbsite, kaolinite, K-mica, and K-feldspar; and the total amounts in the phase assemblage and mole transfers for gibbsite, kaolinite, K-mica, and K-feldspar will be written to the file
ex6A-B.sel
after each calculation. The definitions for SELECTED_OUTPUT remain in effect for all simulations in the run until a new SELECTED_OUTPUT data block is read or until writing to the file is suspended with the identifier
-selected_output
in the PRINT data block.
Table 22.
Selected results for simulation 6A.
[Simulation refers to labels in the input file for simulation 6A. Negative mole transfers indicate dissolution, positive mole transfers indicate precipitation. Simulations 6A1-6A6 refer to label points A-F on figure 7 and table 24. H
+
, hydrogen ion; K
+
, potassium ion; H
4
SiO
4
, silicic acid]
|
Simu-lation
|
K-feldspar mole transfer micro-
moles
|
Log activity
|
|
Mole transfer, micromoles
|
|
Saturation index
|
Point on graph
|
|
H
+
|
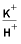
|
H
4
SiO
4
|
|
Gibbs-
ite
|
Kao-
linite
|
K-
mica
|
|
Gibbs-ite
|
Kao-
linite
|
K-
mica
|
K-
feldspar
|
|
6A1
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A
|
|
6A2
|
|
|
|
|
|
|
|
|
|
|
|
|
|
B
|
|
6A3
|
|
|
|
|
|
|
|
|
|
|
|
|
|
D
|
|
6A4
|
|
|
|
|
|
|
|
|
|
|
|
|
|
F
|
|
6A5
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C
|
|
6A6
|
|
|
|
|
|
|
|
|
|
|
|
|
|
E
|
Simulation 6A1 allows K-feldspar to react until equilibrium with gibbsite is reached. This is set up in the EQUILIBRIUM_PHASES input by specifying equilibrium for gibbsite (saturation index equals 0.0) and an alternative reaction to reach equilibrium, KAlSi3O8 (the formula for K-feldspar). A large amount of K-feldspar (10.0 mol) is present to ensure that equilibrium with gibbsite can be obtained. Kaolinite, K-mica, and K-feldspar are allowed to precipitate if they become saturated (which does not occur in this part of the simulation), but they cannot dissolve because they were given zero initial moles in the phase assemblage. The amount of reaction is the dissolution of precisely enough K-feldspar to reach equilibrium with gibbsite. No gibbsite will dissolve or precipitate; the alternative reactant (KAlSi3O8) will dissolve or precipitate in its place. Simulations 6A2-6A4 perform the same calculations for kaolinite, K-mica, and K-feldspar. At other temperatures or using other minerals, a target phase may remain undersaturated regardless of the amount of the alternative reaction that is added because the phase is unstable relative to the other defined phases. If this were the case, the numerical method would find the amount of the alternative reaction that produces the maximum saturation index for the target phase.
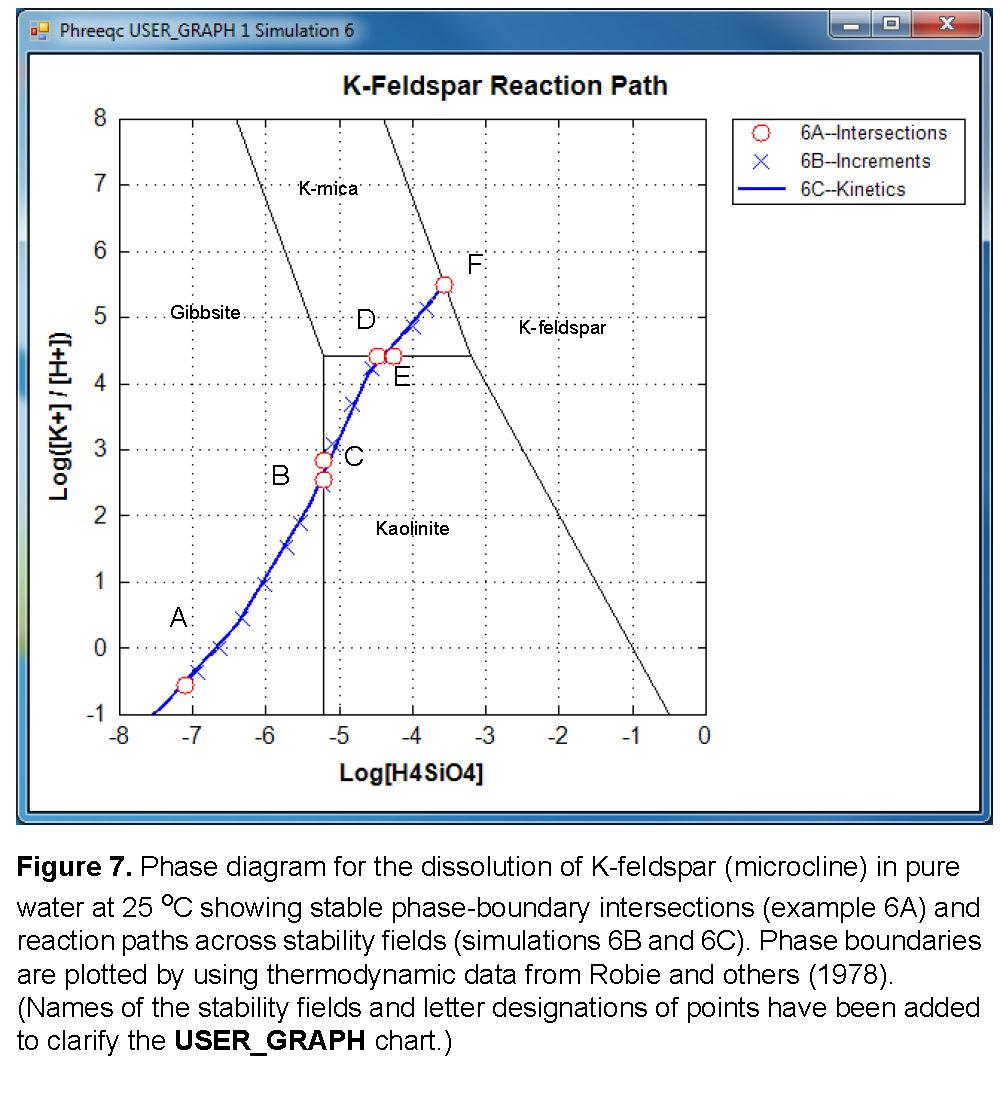
Selected results for simulations 6A1-6A4 are presented in table 22 and are plotted on figure 7 as points A, B, D, and F. The stability fields for the phases, which are based on the thermodynamic data, are calculated and plotted with USER_GRAPH as explained later. At point B, gibbsite starts to be transformed into kaolinite, a reaction that consumes Si. From this point, the reaction path follows the gibbsite-kaolinite phase boundary until all gibbsite is converted (point C), and then crosses the kaolinite field to point D. Similarly, there is a point E on the kaolinite-K-mica phase boundary, where the reaction path starts crossing the K-mica field to point F. Simulations 6A5 and 6A6 (table 21) solve for the two points C and E. In simulation 6A5, point C is calculated by specifying that kaolinite is present at equilibrium, while K-feldspar dissolves until gibbsite is at saturation, but with zero concentration in the phase assemblage. Likewise, simulation 6A6 solves for the point where K-mica is at saturation and present in the phase assemblage, while kaolinite is at saturation, but with zero concentration (point E). Assigning an initial amount of 1 mol to kaolinite in 6A5 and to K-mica in 6A6 is arbitrary, but the amount must be sufficient to reach equilibrium with the mineral.
A simpler approach to determining the reaction path is to react K-feldspar incrementally, allowing the stable phase assemblage among gibbsite, kaolinite, K-mica, and K-feldspar to form at each point along the path. The only difficulty in this approach is to know the appropriate amounts of reaction to add. From points A to F in figure 7, K-feldspar dissolution ranges from 0.03 (simulation 6A1, table 22) to 190.9 mmol (simulation 6A4, table 22). In simulation 6B (table 21) a logarithmic range of reaction increments is used to define the path (solid line) across the phase diagram (fig. 7) from its beginning at gibbsite equilibrium (point A) to equilibrium with K-feldspar (point F). However, the exact locations of points A through F will not be determined with the arbitrary set of reaction increments that are used in simulation 6B (table 21). The reaction path calculated by simulation 6B is plotted on the phase diagram in figure 7 with points A through F from simulation 6A (table 21) included in the set of points.
Finally, in the kinetic approach in simulation 6C (table 21), kinetic dissolution of K-feldspar is followed with time, while the phases gibbsite, kaolinite, and K-mica are allowed to precipitate and redissolve as the kinetic reaction proceeds. SOLUTION 1 is defined to have a small amount of dissolved K-feldspar (1×10
-13
mol). The solution then contains all elements related to phases in EQUILIBRIUM_PHASES, which, although not required for the program to run successfully, eliminates some warning messages.
During the integration of the reaction rates, a simple dissolution rate law was assumed based on transition-state theory:
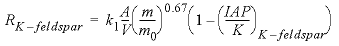 , (20)
, (20)
where R is the rate, mol cm
-2
s
-1
(mole per square centimeter per second);
k
1
is the rate constant, equal to 1×10
-16
mol cm
-2
s
-1
; m is the amount of kinetic reactant, mol; m
0
is the initial amount of kinetic reactant, mol; IAP is the ion activity product; and K is the equilibrium constant.
The KINETICS data block is used to enter specific data for the kinetic simulation. The stoichiometry of the kinetic reaction is the chemical formula of K-feldspar; by default, the name of the rate is assumed to be a phase defined in the PHASES data block and the formula of the phase is used as the stoichiometry of the reaction. It was assumed that the pristine soil contained 10 percent K-feldspar in the form of 0.1 mm cubes, and had 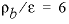 g/cm
3
, so that
A/V
= 136/cm. The value of
g/cm
3
, so that
A/V
= 136/cm. The value of 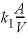 = 1.36×10
-11
mol L
-1
s
-1
(mole per liter per second) is entered in the KINETICS data block with the identifier
-parms
(assuming that 1 kgw = 1 liter), and can be recalled as “PARM(1)” in the Basic rate definition in the RATES data block. It was assumed that the soil had already been weathered to some extent, and that only 90 percent of the initial K-feldspar was left [
-m0
2.16 and
-m
1.94, where
m0
indicates the initial mass
= 1.36×10
-11
mol L
-1
s
-1
(mole per liter per second) is entered in the KINETICS data block with the identifier
-parms
(assuming that 1 kgw = 1 liter), and can be recalled as “PARM(1)” in the Basic rate definition in the RATES data block. It was assumed that the soil had already been weathered to some extent, and that only 90 percent of the initial K-feldspar was left [
-m0
2.16 and
-m
1.94, where
m0
indicates the initial mass
(1 kg soil × 0.1 = 100 g / 278.3 g/mol = 0.359 mol/kg × 6 kg/L = 2.16 mol/L), and
m
is the remaining mass (90 percent of 2.16 is 1.94 mol/L)]. The maximum amount of reaction for any time interval is restricted to 1×10
-6
mol (
-step_divide
1e-6). Time steps (s) are defined with the identifier
-steps
. INCREMENTAL_REACTIONS
true
causes each new time step to start at the end of the previous time step, so that the total time is the sum of all the time steps (= 1.111111×10
8
s).
The rate for K-feldspar dissolution is defined in the form of Basic statements in the RATES data block. To demonstrate some of the features of the Basic interpreter, the Basic program also identifies and saves information at phase transitions, which is printed at the end of the run by using USER_PRINT. The accuracy of locating a phase transition is determined by the user-definable accuracy of the integration. A small tolerance (
-tol
), a large
-step_divide
that is greater than 1 (initial time interval will be divided by this number), or a small
-step_divide
that is less than 1 (specifies maximum moles of reaction) will force smaller time intervals and more accurate identification of phase transitions. In this simulation (6C),
-step_divide
is set to 1×10
-6
, which limits the maximum amount of reaction for any time interval to be less than 1 micromole. Thus, the amount of reaction to reach a phase transition will be identified with an accuracy of 1 micromole. However, limiting the amount of reaction requires smaller time intervals during the integration and, consequently, more time intervals to complete the integration, which increases the CPU time of the run.
The purpose of each part of the Basic program is described in table 23. The functions PUT, GET, and EXISTS are used to manipulate data in static, global storage. The arguments used in the PUT function identify a number and the storage location. For example, PUT(M,i) will place the value of “M” in the location identified by the variable i. EXISTS can be used to determine if a storage location contains a number, and GET is used to retrieve data that have been stored. For example, IF EXISTS(i) then m2 = GET(i) will assign the number in location i to m2 if i contains a number, and do nothing if it does not. Once a number has been stored with PUT, it exists for the remainder of the run, unless it is overwritten with another PUT statement in the same location (that is, with the same set of subscripts). Data stored with PUT can be retrieved by any Basic program defined in RATES, USER_GRAPH, USER_PRINT, and USER_PUNCH. In this simulation (6C), data are stored by the RATES Basic program, and the USER_PRINT Basic program retrieves the data and prints a summary of the phase transitions. Whereas the RATES program is run many times during the kinetic integration of a time step, the USER_PRINT program is run only once at the end of each integration time step.
Table 23. Description of Basic program for K-feldspar dissolution kinetics and identification of phase transitions.
[mol, mole]
|
Line number
|
Purpose
|
|
20
|
Save initial amount of K-feldspar (1.94 mol)
|
|
40-50
|
Integrate K-feldspar dissolution rate over time interval given by TIME.
|
|
90-110
|
Identify greatest amount of K-feldspar present (least amount of reaction) at which gibbsite is saturated.
|
|
160-180
|
Identify greatest amount of K-feldspar present at which kaolinite is saturated.
|
|
200-230
|
Identify greatest amount of K-feldspar present at which kaolinite is saturated, but gibbsite is absent.
|
|
250-280
|
Identify greatest amount of K-feldspar present at which K-mica is saturated.
|
|
300-330
|
Identify greatest amount of K-feldspar present at which K-mica is saturated, but kaolinite is absent.
|
|
350-380
|
Identify greatest amount of K-feldspar present at which K-feldspar is saturated.
|
|
1000
|
Save integrated reaction.
|
|
1010
|
End of Basic program
|
|
1500-1560
|
Subroutine for saving values for phase transitions. If amount of K-feldspar is greater than current saved value for the index
i
, save amount of K-feldspar, cumulative time, log activity ratio of potassium ion divided by hydrogen ion, and log activity of silicic acid.
|
See Phase transitions identified by the RATES Basic program and printed to the output file by the USER_PRINT Basic program in simulation 6C, which simulates the kinetic dissolution of K-feldspar. gives the phase transitions encountered by the end of the last time step of simulation 6C. For each phase transition, the time at which the phase transition occurred, the total amount of K-feldspar that has reacted, and the coordinates of the transition on figure 7 are given. Although the values in table 24 are. approximate, the amount of K-feldspar and the coordinates of the transition can be compared with table 22 As expected, the approximate mole transfers to reach the phase transitions in table 24 (column 3) are within 1 micromole of the values in table 22 (column 2).
Table 24. Phase transitions identified by the
RATES
Basic program and printed to the output file by the
USER_PRINT
Basic program in simulation 6C, which simulates the kinetic dissolution of K-feldspar.
----------------------------------User print-----------------------------------
|
|
Transition Time K-feldspar LA(K/H) LA(H4SiO4)
|
transfer
|
(umoles)
|
A: Gibbsite 1100 1.4048e-001 3.5642e-001 -6.3763e+000
|
B: Gibbsite -> Kaolinite 1.7434e+005 2.2064e+000 2.5575e+000 -5.1950e+000
|
C: Gibbsite -> Kaolinite 2.3929e+005 3.0284e+000 2.8317e+000 -5.1945e+000
|
D: Kaolinite -> K-mica 1.5967e+006 2.0194e+001 4.4080e+000 -4.4630e+000
|
E: Kaolinite -> K-mica 2.6017e+006 3.2848e+001 4.4087e+000 -4.2499e+000
|
F: K-mica -> K-feldspar 4.7638e+007 1.9074e+002 5.4868e+000 -3.5536e+000
|
The SELECTED_OUTPUT data block specifies that a new selected-output file will be used for this simulation,
ex6C.sel
, and all printing to the selected-output file is eliminated (
-reset
false). The USER_PUNCH data block causes two columns to be written to each line of the selected-output file, the log of the ratio of the activities of potassium ion to hydrogen ion and the log activity of silicic acid. The data are written after each time step has been simulated (
-steps
, KINETICS data block). See Results written to the selected-output file by the USER_PUNCH Basic program in simulation 6C, which simulates the kinetic dissolution of K-feldspar. shows the results written to
ex6C.sel
.
The phase boundaries in figure 7 are plotted with USER_GRAPH at the end of the file. First, a dummy phase “K_H” is defined that will provide the activity ratio of K+ and H+ in the solution, which is plotted on the y-axis. The
-log_k
of zero for the reaction is the default value in PHREEQC and may be omitted. The saturation index of a solution for this phase is given by log([K+] / [H+]), and can be obtained with SI("K_H") in a Basic program. Next, four solutions are defined for the points that delimit the phase boundaries, going from top to bottom and from left to right. USER_GRAPH connects the points with a black line, without symbols, and without entry in the legend (no
-
headings). After the END, another four solutions are defined for the phase boundaries from top to bottom and from right to left, and another curve is drawn by redefining line 10 in USER_GRAPH (in this way avoiding connecting the last bottom-right point with the new top-right point). Note that the text is compacted in this part of the input file by concatenating lines with semicolons, “;”.
Table 25. Results written to the selected-output file by the
USER_PUNCH
Basic program in simulation 6C, which simulates the kinetic dissolution of K-feldspar.
[“\t” indicates a tab character]
pH+log[K]\t log[H4SiO4]\t
|
-6.0002e+000\t -1.2524e+001\t
|
-1.8975e+000\t -8.4212e+000\t
|
-8.5318e-001\t -7.3798e+000\t
|
3.5742e-001\t -6.3763e+000\t
|
2.1790e+000\t -5.3817e+000\t
|
4.1326e+000\t -4.6001e+000\t
|
5.2599e+000\t -3.7183e+000\t
|
5.4872e+000\t -3.5533e+000\t
|
8.0000e+000\t -6.3924e+000\t
|
4.4080e+000\t -5.1950e+000\t
|
4.4080e+000\t -3.1935e+000\t
|
-1.0000e+000\t -4.9484e-001\t
|
8.0000e+000\t -4.3909e+000\t
|
4.4080e+000\t -3.1935e+000\t
|
4.4080e+000\t -5.1950e+000\t
|
-1.0000e+000\t -5.1950e+000\t
|
| Next || Previous || Top |
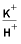

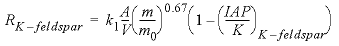 , (20)
, (20)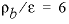 g/cm
3
, so that
A/V
= 136/cm. The value of
g/cm
3
, so that
A/V
= 136/cm. The value of 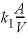 = 1.36×10
-11
mol L
-1
s
-1
(mole per liter per second) is entered in the
= 1.36×10
-11
mol L
-1
s
-1
(mole per liter per second) is entered in the