EXCHANGE_SPECIES
This keyword data block
is used to define a half-reaction and relative log K for each exchange
species. Normally, this data block is included in the database file and only
additions and modifications are included in the input file.
Example
data block
Line 0: EXCHANGE_SPECIES
Line 1a: X- = X-
Line 2a: log_k 0.0
Line 1b: X- + Na+ = NaX
Line 2b: log_k 0.0
Line 3: -gamma 4. 0.075 0.1
Line 1c: 2X- + Ca+2 = CaX2
Line 2c: log_k 0.8
Line 4: -davies
Line 1d: Xa- = Xa-
Line 2d: log_k 0.0
Line 1e: Xa- + Na+ = NaXa
Line 2e: log_k 0.0
Line 1f: 2Xa- + Ca+2 = CaXa2
Line 2f: log_k 2.0
Explanation
Keyword for the data
block. No other data are input on the keyword line.
Association reaction
for exchange species. The defined species must be the first species to the
right of the equal sign. The association reaction must precede any identifiers
related to the exchange species. Master species have an identity reaction (Lines
1a and 1d).
log_k
--Identifier for log K at 25 °C. Optionally, -log_k ,
logk , -l [
og_k ], or -l [ ogk ].
log
K --Log K at 25 °C for the reaction. Unlike log K
for aqueous species, the log K for exchange species is implicitly
relative to a reference exchange species. In the default database file, sodium
(NaX) is used as the reference and the reaction X
- + Na + = NaX is given a log K
of 0.0 (Line 2b). By subtracting the reaction for NaX
in Line 1b twice from the reaction for CaX2 in Line 1c, it follows that log K
for the reaction in Line 2c is numerically equal to log K for the
reaction 2NaX + Ca +2 = CaX 2 +
2Na + .
The identity reaction for a master species has log K of 0.0 (Lines 2a
and 2d); reactions for reference species also have log K of 0.0 (Lines
2b and 2e). Default is 0.0.
Line
3: -gamma Debye-Hückel a, Debye-Hückel b, active_fraction_coefficient
-gamma
--Indicates WATEQ Debye-Hückel equation will be used
to calculate an activity coefficient for the exchange species if the aqueous
model is an ion-association model (see -exchange_gammas
in the EXCHANGE data block for
information about activity coefficients when using the Pitzer or SIT aqueous
models). If -gamma or -davies
is not input for an exchange species, the activity of the species is equal to
its equivalent fraction. If -gamma is entered, then an
activity coefficient of
the
form of WATEQ (Truesdell and Jones, 1974),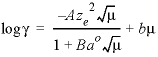 
,
is multiplied times the equivalent fraction to obtain activity for the exchange
species. In this equation, 
is the activity
coefficient, 
is ionic strength
(mol/L [mole per liter], assumed to be equal to mol/kgw
[mole per kilogram water]), A and B are constants at a given
temperature and pressure, 
is the number of
equivalents of exchanger in the exchange species, and 
and
b are ion-specific parameters. Optionally, gamma or -g
[ amma ].
Debye-Hückel a --Parameter ao in the WATEQ activity-coefficient equation.
Debye-Hückel b --Parameter b in
the WATEQ activity-coefficient equation.
active_fraction_coefficient
--Parameter for changing log_k as a function
of the exchange sites occupied (Appelo, 1994a). The active-fraction model is
useful for modeling sigmoidal exchange isotherms and proton exchange on organic
matter (see http://www.hydrochemistry.eu/exmpls/a_f.html, accessed June 25,
2012).
-davies --Indicates the Davies
equation will be used to calculate an activity coefficient. If -gamma
or -davies is not input for an
exchange species, the activity of the species is equal to its equivalent
fraction. If -davies is entered,
then an activity coefficient of the form of the Davies equation, 
, is multiplied times the equivalent
fraction to obtain activity for the exchange species. In this equation, 
is the activity coefficient, 
is ionic strength, A is a
constant at a given temperature, and 
is
the number of equivalents of exchanger in the exchange species. Optionally, davies or -d
[ avies ].
Notes
Lines 1 and 2 may be
repeated as necessary to define all of the exchange
reactions, with Line 1 preceding Line 2 for each exchange species. One identity
reaction that defines the exchange master species (in the Example data block,
Lines 1a and 2a, 1d and 2d) and one reference half-reaction are needed for each
exchanger. The identity reaction has a log K of 0.0. The reference
half-reaction for each exchanger also will have a log K of 0.0 (in the
Example data block, Lines 1b and 2b, 1e and 2e); in the default database file
the reference half-reaction is Na + + X - = NaX. Multiple exchangers may be defined simply by defining
multiple exchange master species and additional half-reactions involving these
master species, as in this Example data block.
Activities of exchange
species may be expressed as equivalent or mole fractions of the species
(Gaines-Thomas or Vanselow convention, respectively), or as fractions of the
exchange sites occupied (Gapon convention). All three
conventions can be used in PHREEQC (see
http://www.hydrochemistry.eu/pub/ap_pa02.pdf, accessed June 25, 2012). In the
databases, the Gaines-Thomas convention is used.
Cation exchange
experiments with heterovalent exchange in which the
salinity of the solutions is varied (for example, exchange of 2Na +
for Ca2+ at varying Cl- concentrations) can be modeled better when exchange is
calculated with molal concentrations for solute species instead of activities.
This implies that the activity coefficients of solute cations and exchangeable
species are the same, perhaps because a large part of cation exchange in soils
and sediments takes part in the electrostatic double layer. Accordingly,
PHREEQC permits the activity coefficient for exchangeable species to be defined
in the same way as the solute species. The -gamma identifier
allows the equivalent fraction to be multiplied by an activity coefficient by
using the WATEQ Debye-Hückel equation. Similarly,
when using the llnl.dat database, -llnl_gamma
can be used to multiply the equivalent fraction by the activity coefficient
that is defined according to the conventions of the llnl.dat database.
The Davies equation can be used to calculate the activity coefficient of the
exchange species by specifying the -davies
identifier. The use of these equations is strictly empirical and is motivated
by the observation that these activity corrections provide a better fit to some
experimental data.
Temperature dependence
of log K can be defined with the standard enthalpy of reaction ( -delta_h
) using the Van’t Hoff equation or with an analytical expression ( -analytical_expression ). Sometimes it is useful to
offset a log K from zero for parameter fitting, or to account for dependencies
among log K values, in which case the -add_log_k
identifier can be used to add the value defined by a named analytical
expression (MIX_EQUILIBRIUM_PHASES)
to the log K of the exchange species. See SOLUTION_SPECIES for examples.
The identifier -no_check can be used to disable checking charge
and elemental balances (see SOLUTION_SPECIES)
and allows the Gapon exchange convention to be used
(See http://www.hydrochemistry.eu/a&p/6/exch_phr.pdf, accessed June 25,
2012).
Example
problems
The keyword EXCHANGE_SPECIES
is used in example problems 12,
13, 18, and 21. See also the databases Amm.dat , iso.dat , llnl.dat ,
phreeqc.dat , pitzer.dat , and wateq4f.dat .
Related
keywords
EXCHANGE, EXCHANGE_MASTER_SPECIES, SAVE exchange , SOLUTION_SPECIES, and USE exchange .