USGS Surface Water Information
Selected USGS Surface-Water Publications
New & Noteworthy
USGS in Your StateUSGS Water Science Centers are located in each state. ![[Map: There is a USGS Water Science Center office in each State.]](http://www.usgs.gov/frameworkfiles/includes/imagemaps/usmapsmall.gif)
Other Water SitesPDF Reader!Documents are presented in Portable Document Format (PDF); the latest version of Adobe Reader or similar software is required to view it. Download the latest version of Adobe Reader, free of charge. |
Open-File Report 99-221
By E.F. Hubbard, K.G. Thibodeaux, and Mai N. Duong | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Price AA current meter | Price pygmy current meter | ||
|---|---|---|---|
| Velocity, in feet per second | Accuracy criterion, in percent | Velocity, in feet per second | Accuracy criterion, in percent |
These accuracy criteria are based on much experimental data and have a statistical basis. The criteria are set at about 2 standard deviations of published current-meter calibration data (Smoot and Carter, 1968; Schneider and Smoot, 1976; and W.H. Kirby, written commun., 1998). Current meters that are subsequently calibrated meet the criteria if their velocities predicted from the appropriate standard rating falls within the plus or minus limits of the true velocity, which is measured during the calibration process. About 95 percent of current meters are expected to meet the criteria shown in table 1, if the calibration data are normally distributed and the standard rating is an accurate measure of the average responsiveness of the meters tested. International standard "Assessment of uncertainty in the calibration and use of flow measurement devices-Part 1: Linear calibration relationships," which was issued by The International Organization for Standardization (1989), also establishes the 2-standard-deviation criteria as being appropriate for calibration of current meters.
The accuracy criteria for whether a meter passes or fails in regard to the true velocity are applied with considerable judgement and latitude. If the standard rating does not predict (based on the rotational velocity of the bucket wheel) the actual velocity within the criteria at one calibration- data point, the possibility of a laboratory error is explored. If miscounting by the instrument that counts the bucket-wheels rotations is detected when inspecting the data, that data point is deleted or corrected to permit the meter to pass. If there are still one or more calibration-data points that are not within the criteria but are close (within about one tenth of a percent), the relationship between rotational velocity and water velocity that is defined by the individual meter's calibration data is generated. If this resulting equation (or equations in the case of the AA meters) plots within the accuracy criteria, the meter is judged to have passed, even if a calibration-data point or two is outside the limits. Finally, the rounding of the accuracy criteria as used in the laboratory software is such that the limits are slightly larger than those shown in table 1. For example, the working criteria for the three faster velocities for the AA meter effectively has been 1.1 percent, instead of 1.0 percent (table 1).
The USGS counterparts in Environment Canada do not use standard ratings. Although they principally use the AA and pygmy meters, the Canadians feel it necessary to rate each meter individually. The meters that the Canadians use are periodically recalled to their hydraulic laboratory in Burlington, Ontario, to be rebuilt and re-rated (DeZeeuw and Bil, 1975). The laboratory also performs this function for meters owned by Canadian provinces, hydro-power companies, and others.
Instrument error is only one of several significant errors that may contribute to the overall error of a discharge measurement. Sauer and Meyer (1992) found that most measurements of discharge by current meters will have standard errors ranging from 3 to 6 percent. Poor measuring conditions (such as very slow water velocities or shallow depths) or improper procedures of meter use, however, can result in much larger errors. They cited important sources of error--other than the error contributed by the current meter--such as the measurement of depth, the pulsation of flow, the vertical distribution of velocities, the measurement of horizontal angles, and the computations involving the horizontal distribution of velocity and depth (insufficient number of or inadequate measuring subsections).
Sauer and Meyer estimated the total error of discharge measurements by taking the square root of the sum of the squares of the individual errors contributed by the various sources of error. The error associated with the current meter, which Sauer and Meyer termed "instrument error", was relatively small (0.3 percent) for AA meters used under ideal measuring conditions and following the recommended field procedures. For pygmy meters, the instrument error they used was still relatively small at 0.8 percent for a wading measurement with good field conditions. Their analysis properly used the standard error of estimate, which is 1 standard deviation of the calibration data used to develop the standard rating. Sauer and Meyer did not consider the case of a meter whose difference from the standard rating is near to or falls outside of the accuracy criteria, which is 2 standard deviations. Such a meter could contribute an instrument error up to about twice as large as they used.
In poorer field conditions where the velocity is slow, Sauer and Meyer found meter error to be a large source of error with respect to the other sources. Here again, they used the standard error of 1, not 2, standard deviations as the instrument error.
The errors associated with individual discharge measurements contribute to the error of the rating curve, which is the graphical relationship between stage and discharge for a streamflow gaging station. The rating-curve error is incorporated directly in the discharges that are computed and published for a station.
If several meters were employed in the development of the rating curve, instrument errors might off-set each other. This does not always happen in practice, however. Sometimes long periods go by when one meter is predominately used to define the rating curve. Thus, any error in velocity data that is introduced by a current meter would be of concern.
In 1988, the Office of Surface Water began the Meter-Exchange Program. One of the purposes of the program was to select meters being used in the field for calibration in the hydraulic laboratory tow tank. The reason for the calibration was to determine the accuracy of current meters as they are actually used in the field. The meters were selected by USGS technical review teams as they periodically reviewed the surface-water programs in field offices. The team members were asked to either select the meters at random or, if a meter in particularly poor physical condition was discovered, on the basis of appearance.
Current meters received in the hydraulic laboratory under this program were first calibrated without instrument adjustments or repairs. These calibration data of the "as-received" meters were retained as representative of the accuracy of meters being used in the field. Afterwards, the meters were repaired, adjusted, and recalibrated to ensure they fit within the accuracy criteria of the standard rating (table 1). The recalibrated meters were exchanged for other current meters selected during subsequent reviews. This program has continued until the present (1999).
Through the Meter-Exchange Program, 128 AA and 125 pygmy meters have been calibrated (table 2). The results of the calibrations indicated that 46 AA and 74 pygmy meters failed to meet the accuracy criteria. Assuming that the calibration data average the same as predicted by the standard rating equations and are distributed normally, then only about 5 percent of the current meters should fall outside the 2-standard-deviation accuracy criterion. The actual failure rates, which are 36 percent for AA meters and 59 percent for pygmy meters, are unacceptably high.
Although the term, "failure rate", is used to describe the percentage of current meters that did not fall with the accuracy criteria of the true velocities measured at calibration, it does not imply that the meters that failed were faulty or operated improperly. Almost all of the meters, in fact, operated satisfactorily. The standard ratings, however, did not predict the responsiveness to water velocity of the meters that failed within the established accuracy criteria. In other words, the bucket wheels of these meters turned unacceptably slower or faster for a given water velocity, causing the velocitiees estimated by the standard ratings to be outside of the accurcy limits around the true velocity.
The high failure rates gave rise to a concern that the meters selected because of poor physical condition were biasing the calibration results. To investigate this concern, the calibration data were divided into three groups: meters selected at random, meters selected non-randomly because of poor appearance, and meters for which there is no information concerning the basis for selection. These data are summarized in table 2.
Table 2: Results of the Meter-Exchange Program through 1998| ALL METERS | |||
|---|---|---|---|
| Meter Type | No. of Meters Meeting Accuracy Criteria |
No. of Meters Failing to Meet Accuracy Criteria |
Percent Failing |
| AA | 82 | 46 | 36 |
| Pygmy | 51 | 74 | 59 |
| METERS SELECTED AT RANDOM | |||
| Meter Type | No. of Meters Meeting Accuracy Criteria |
No. of Meters Failing to Meet Accuracy Criteria |
Percent Failing |
| AA | 65 | 35 | 35 |
| Pygmy | 40 | 62 | 61 |
| METERS HAVING NON-RANDOM SELECTIONS (Poor Physical Condition) | |||
| Meter Type | No. of Meters Meeting Accuracy Criteria |
No. of Meters Failing to Meet Accuracy Criteria |
Percent Failing |
| AA | 9 | 8 | 47 |
| Pygmy | 8 | 4 | 33 |
| METERS HAVING UNKNOWN SELECTION CRITERIA | |||
| Meter Type | No. of Meters Meeting Accuracy Criteria |
No. of Meters Failing to Meet Accuracy Criteria |
Percent Failing |
| AA | 8 | 3 | 27 |
| Pygmy | 3 | 8 | 73 |
There appears to be little difference in the failure rate among the meters in the three categories shown in table 2. The exceptions are that the non-randomly selected AA meters had a somewhat higher rate of failure than that of other AA-meter categories, and the non-randomly selected pygmy meters had a lower rate of failure than that of other pygmy-meter categories. Perhaps technical reviewers were better able to visually discern problems with the AA meters than with the pygmy meters. The physical appearance of a meter, however, is not necessarily a good indicator of whether the meter will fail or meet the accuracy criteria. Even a spin test of a meter is not a good indicator of whether a meter will pass or fail (K.G. Thibodeaux, oral commun., U.S. Geological Survey, 1999). Thibodeaux cites instances of AA meters that had timed spin tests of about 1 minute that met the accuracy criteria, even though this time is well below the minimum spin-test standard of 2 minutes (Hubbard and Barker, 1995).
Because the failure rates of meters chosen at random were virtually the same as that for all three groups combined, those meters chosen on non-random and unknown bases are deemed representative of the entire group and, probably, of the population of current meters used by the USGS. Thus, all the calibration data, regardless of the selection criteria, are used in this analysis.
The apparent causes of meters failing to meet the accuracy criteria were diverse. The physical conditions noted for the meters that failed and the corrective action taken was recorded for each meter that failed. Based on experiences in rebuilding and calibrating current meters in the laboratory, the following general observations are provided:
Tables 3 and 4 summarize the results of the calibration of meters in an "as-received" condition. These statistics represent all meters from the Meter-Exchange Program, although a few individual calibration runs were deleted from the data as spurious outliers. (Calibration data from forward and reverse directions at each nominal velocity were averaged for individual meters to minimize the effects of currents in the tow tank. Thus, the term "calibration run" represents both forward and reverse directions at one of the calibration velocities.)
The average differences and prediction intervals in tables 3 and 4 are calculated to compare with the established accuracy tolerances (table 1) and with the instrument errors that are assumed when estimating overall discharge-measurement error. The statistics are based on the difference, for an individual meter, between the velocity estimated by the standard rating, using the rotational velocity of the bucket wheel, and the measured (true) velocity for each calibration run (forward and reverse averaged). Thus, for all AA meters at a calibration velocity of 0.25 fps (table 3, first row, col. 1), the average difference of the velocities estimated using the standard rating from the actual velocities is -1.06 percent (col. 2). In column 3, the standard deviation of all the individual meter differences is listed for each calibration velocity. Prediction intervals at 1 standard deviation are shown in column 4. The standard deviation used to define the prediction interval corresponds to the standard deviation of the difference between a non-sampled meter's standard- rating velocity estimate and the true velocity. The prediction interval is equal to the square root of the sum of the variance of the individual differences and the variance of the average difference. The prediction intervals listed in column 5 correspond to 2 standard deviations.
Table 3: Calibration data for 128 Price AA meters, expressed in difference of standard rating velocity estimates from true velocities| Average calibration velocity, in feet per second
(1) |
Average difference, in percent (2) |
Standard deviation, in percent (3) |
Prediction interval at 1 stnadard deviation, in percent
(4) |
Prediction interval at 2 standard deviations, in
percent (5) |
||
|---|---|---|---|---|---|---|
| 0.25 | -1.06 | 2.56 | -3.63 | 1.51 | -6.20 | 4.08 |
| 0.50 | -0.18 | 1.05 | -1.23 | 0.87 | -2.29 | 1.93 |
| 0.75 | -0.10 | 0.84 | -0.94 | 0.74 | -1.79 | 1.59 |
| 1.10 | -0.41 | 0.84 | -0.94 | 0.74 | -1.79 | 1.59 |
| 1.51 | -0.51 | 0.88 | -1.39 | 0.37 | -2.28 | 1.26 |
| 2.22 | -0.50 | 0.92 | -1.42 | 0.42 | -2.35 | 1.35 |
| 5.01 | -.51 | 0.95 | -1.46 | 0.44 | -2.42 | 1.40 |
| 8.01 | -0.66 | 0.94 | -1.60 | 0.28 | -2.55 | 1.23 |
At calibration velocities faster than 1 fps, the AA-meter bucket wheels turned 0.41 to 0.66 percent slower than estimated using the standard rating (table 3, col. 2). That is, the meters turned more slowly than expected for a given true velocity and, thus, would yield a velocity from the standard rating table that is slower than the true velocity. On the other hand, the pygmy meters, generally turned faster than predicted by the standard rating, yielding velocities as much as 1.32 percent faster than the true velocity (table 4, col. 2).
Table 4: Calibration data for 125 Price pygmy meters, expressed in difference of standard rating velocity estimates from true velocities| Average calibration velocity, in feet per second
(1) |
Average difference, in percent (2) |
Standard deviation, in percent (3) |
Prediction interval at 1 stnadard deviation, in percent
(4) |
Prediction interval at 2 standard deviations, in
percent (5) |
||
|---|---|---|---|---|---|---|
| 0.25 | -1.40 | 4.07 | -5.49 | 2.69 | -9.57 | 6.77 |
| 0.50 | 0.22 | 1.72 | -1.51 | 1.95 | -3.23 | 3.67 |
| 0.75 | 0.81 | 1.43 | -0.63 | 2.25 | -2.06 | 3.68 |
| 1.51 | 0.72 | 1.68 | -0.97 | 2.41 | -2.65 | 4.09 |
| 2.21 | 1.17 | 1.61 | -0.45 | 2.79 | -2.06 | 4.40 |
| 3.01 | 1.32 | 1.63 | -0.32 | 2.96 | -1.95 | 4.59 |
At calibration velocities of 0.75 fps and faster, the standard deviations of the differences from the true velocity are 0.84 to 0.95 percent for the AA meter (table 3, col. 3). Assuming a normal distribution of the average-difference data, about two-thirds of calibration-run results for untested meters are expected to fall within the prediction interval (col. 4).
About 95 percent of the AA-meter calibration data are expected to be within the prediction interval at 2 standard deviations of the mean. (The mean is shown as the average difference in table 3 col. 2.) For a calibration velocity of 2.22 fps the prediction interval at 2 standard deviations goes from -2.35 to +1.35 percent (col. 5). The range of this prediction interval is more than that of the established accuracy tolerance interval of plus or minus 1.0 percent shown in table 1. For AA meters from the Meter-Exchange Program at calibration velocities of 0.75 fps and faster, the prediction intervals at 2 standard deviations for the standard rating range from -2.55 to +1.59 percent (table 3, col. 5) of the true velocities. This variability in calibration data and the differences from the true velocity for AA meters can be seen in figure 2.
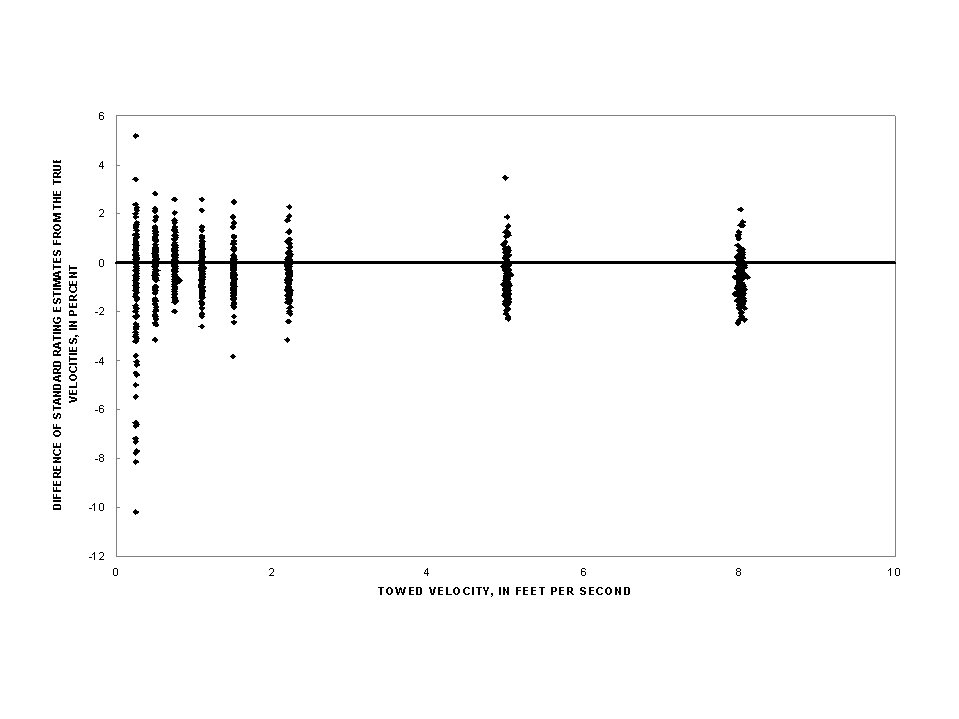
Figure 2: Calibration results for AA meters in the Meter-Exchange Program.
For pygmy meters at a calibration velocity of 2.21 fps, the prediction interval at 1 standard deviation for the standard rating is from -0.45 to +2.79 percent of true velocities and from -2.06 to +4.40 percent at 2 standard deviations (col. 5). The prediction interval at 2 standard deviations is more than the plus or minus 1.5 percent interval allowed for pygmy meters at this velocity (table 1). At calibration velocities of 0.75 fps and faster, pygmy meters from the Meter-Exchange Program have a prediction interval at 2 standard deviations that ranges from -2.65 to +4.59 percent of the true velocities (table 4, col. 5).
Similar to the AA meters, the pygmy-meter responsiveness exhibits both an average difference (shown in table 4, col. 2) and more variability (col. 5) than is permitted by the tolerances associated with the standard rating (table 1). This variability in calibration data and the differences from the true velocity for pygmy meters can be seen in figure 3.
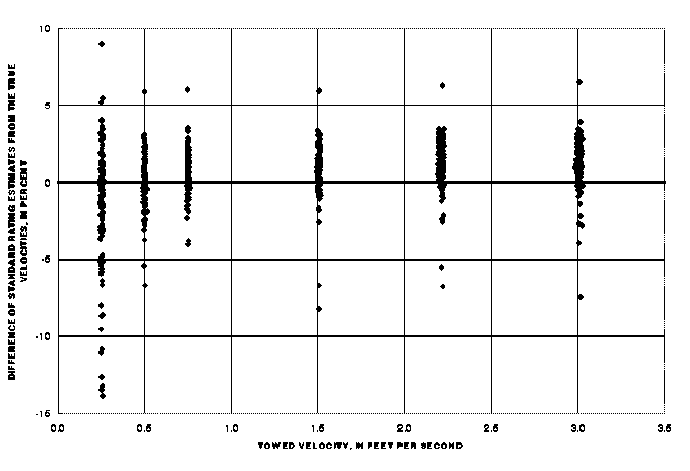
Figure 3: Calibration results for pygmy meters in the Meter-Exchange Program.
The standard rating tables are expected to predict calibration data for current meters with a small difference from the true velocity. This expectation of a small variation of calibration data around the true velocities, which is based on the results of Smoot and Carter (1968), led Sauer and Meyer (1992) to use an instrument error for AA meters of 0.3 percent for velocities of 2.3 fps and faster. The Meter-Exchange Program calibration data show that AA meters from the field calibrated at 2.2 fps have a average difference from the standard rating of -0.50 percent (table 3, col. 2) and a standard deviation of 0.92 percent (col. 3). The prediction interval of the standard rating table at 1 standard deviation for this group of AA meters ranges from -1.42 to +0.42 percent of the true velocity at 2.22 fps (col. 4). This range in error is significantly larger than the plus or minus 0.3 percent used in Sauer and Meyer's equations for velocities of 2.3 fps and faster.
Similarly, on the basis of data from Schneider and Smoot (1976), Sauer and Meyer (1992), used instrument errors for pygmy meters that ranged from 5.14 percent at 0.25 fps to 1.42 percent at 3.0 fps. The pygmy meters, like the AA meters, that were tested in the Meter-Exchange Program had an average difference (bias) from the standard rating. These meters also had a standard deviation that was larger than expected. The prediction interval at 1 standard deviation ranges from as much as -5.49 percent of the true velocity at 0.25 fps to +2.96 percent at 3.01 fps (table 4, col. 4). The difference in velocities predicted by the standard ratings for field AA and pygmy meters from true velocities is larger than the instrument errors used by Sauer and Meyer (1992).
The changes in average responsiveness of meters that have occurred since the standard ratings were implemented probably result from small changes in the physical dimensions of bucket wheels or in other factors affecting meter responsiveness. The larger variability in responsiveness that is seen in the Meter-Exchange Program meters as contrasted to the meters on which the standard ratings are based may result from the treatment that the two groups of meters had received and from the sources of manufacture. For example, the results of calibration data cited in Smoot and Carter (1968) are from AA current meters in new or nearly new condition, and apparently, from a few manufacturing runs. The data from the Meter-Exchange Program are from a sample of meters subjected to normal wear and tear over a varying numbers of years. These meters came from many manufacturing runs. These contrasts may explain the larger variability seen in the calibration data from the Meter-Exchange Program. Nevertheless, the concept of using standard rating tables is predicated on having meters in the field that measure water velocity within accepted accuracy tolerances of the true velocity.
For AA meters, Sauer and Meyer used a standard error of 0.3 percent to compute the overall error of a good cable-suspension as 2.4 percent1. Had the larger value of -1.42 percent (table 3, col. 4) from the Meter-Exchange Program data at 2.22 fps been used, the error of this measurement would have increased to 2.8 percent. These calculations are made below:
the constant value 0.75 is the se, in percent, associated with the systematic errors in the measurement of width, depth and velocity.
If Si is increased from 0.3 to 1.42 percent, then:
For pygmy meters, Sauer and Meyer used an instrument error of 0.8 percent to compute an overall discharge-measurement error of 4.0 percent for a typical good wading measurement with an average velocity of 1.5 fps. At a calibration velocity of 1.5 fps, pygmy meters from the Meter- Exchange Program have a prediction interval at 1 standard deviation from the true velocity ranging up to 2.41 percent (table 4. col. 4). Using this larger percentage in the equation results in an increase in the overall error of the example pygmy meter wading measurement to 4.6 percent.
Thus, the increase in estimated error for a good cable-suspension discharge measurement made with a AA meter is only 0.4 percent (2.8 percent-2.4 percent). The increase in estimated error for a good wading measurement made with a pygmy meter is 0.6 percent. These increases in overall measurement error are inconsequential, except for the fact that both groups of meters, AA's and pygmys, have average differences from the standard ratings. These differences affect the streamflow gaging station stage-discharge ratings, which results in systematic errors in USGS records of streamflow. The errors in streamflow are small, being similar to the average differences in col. 2 of tables 3 and 4, but they could be largely eliminated. Two ways to eliminate the systematic errors are to develop new standard rating tables that more nearly reflect the average responsiveness of meters or to use individual current-meter rating tables.
The Meter-Exchange Program data show that the standard-rating fails to predict the water velocities measured by 36 percent of the Price AA meters and 59 percent of the Price pygmy within the accepted accuracy criteria of about 2 standard deviations from the true velocities. Only about 5 percent of the meters would be expected to have predicted velocities that fall outside the accuracy criteria. Thus, the rate of failure is much higher than was envisioned when the standard rating tables for the meters were prepared.
Even though the failure rate is high, the resultant error in velocity measurement is small. For the AA-meter calibration data, which has less variability than the pygmy-meter data, the maximum difference from velocities predicted by the standard rating at 2 standard deviations is about -2.6 percent in the range of 0.75 to 8.00 fps. For pygmy meters, the maximum average difference from the standard rating is about +4.6 percent at calibration velocities ranging from 0.75 to 3.00 fps.
Error associated with the current meter is only one of the errors encountered in measuring discharge. For this reason, instrument error has to be relatively large to increase the overall error of a discharge measurement more than the +/- 5 percent level, which is assumed to be the maximum error when "good" conditions are indicated on the front of the measurement notes sheet. For velocities of 0.75 to 8.00 fps, it is very unlikely that the size of errors in velocity seen in the Meter-Exchange Program AA-meter calibration data would result in a discharge measurement, which was made under good conditions, having an overall error exceeding 5 percent. It would be somewhat unlikely for the discharge-measurement error to exceed 5 percent when using a pygmy meter under similar measuring conditions. Under worse measuring conditions, except for low velocities, the meter error would have even less influence on the overall error of the discharge measurement.
Be that as it may, for a gaging station where a hydrographer consistently uses a meter, which has a difference in response of, say, 2 to 4 percent from that predicted by the standard rating, the stage-discharge rating for that gage will have similar error. Such an error could add up to thousands of acre-feet of water that were unaccounted for or that were over reported. An error of this size might throw off a flood forecast or otherwise mislead users of USGS data. The USGS has an obligation to reduce these errors, if it can reasonably do so.
Through the Meter-Exchange Program, 253 Price type AA and pygmy meters were calibrated in the 11-year period since its inception in 1988--about 11 or 12 meters of each type per year. This annual sample of calibrated meters is too small to evaluate whether the average responsiveness of meters used in the field is changing from year to year. The sample may also be too small over a period of a few years to identify causative factors in meters that fail to meet the accuracy criteria. Today, technical reviewers do not have the data needed to help identify causative factors of the velocity-accuracy problems in the meters they select. Such factors might include age, amount or frequency of use, environmental conditions under which the meters are used, instrument-care procedures, and so forth. Even since the inception of the program in 1988, the entire sample is too small to differentiate among selection-criteria categories, such as poor physical condition or random selection.
Meters returned to the hydraulic laboratory for calibration are almost always returned to the Meter-Exchange Program after the repairs and adjustments are made. The subsequent recalibration data has shown that these rebuilt and adjusted meters, as a group, have less variability in response than when the same group of meters were calibrated in an "as-received" condition. Thus, better procedures for current-meter maintenance in the field would prevent some of the problems found in the Meter-Exchange Program.
DeZeeuw, C., and Bil, C., 1975, Repair and maintenance manual of the Price current meter, Canada Centre for Inland Water, National Calibration Service, Burlington, Ontario, p 5.
Hubbard, E.F., and Barker, Allison Randolph, 1995, Selected surface-water technical memorandums of the U.S. Geological Survey: U.S. Geological Survey Open-File Report 95-354, p. 201.
International Organization for Standardization, 1989, Assessment of uncertainty in the calibration and use of flow measurement devices-Part 1: Linear calibration relationships: ISO 7066-1: 1989 (E), 39 p.
International Organization for Standardization, 1976, Liquid flow measurement in open channels- Calibration of rotating-element current-meters in straight open tanks: ISO 3455-1976, 8 p.
Schneider, V. R., and Smoot, G. F., 1976, Development of a standard rating for the Price Pygmy current meter: U.S. Geological Survey Journal of Research, vol. 4, no. 3, p. 293-297.
Smoot, G. F., and Carter, R. W., 1968, Are individual current meter ratings necessary? American Society of Civil Engineers Journal of the Hydraulics Division, 94 (HY2), p. 391-397.
Sauer, V. B., and Meyer, R. W., 1992, Determination of error in individual discharge measurements: U.S. Geological Survey, Open-File Report 92-144, 21p.
1The computations are made using equation 14, which appears on page 17 of Sauer and Meyer (1992). The procedure is basically taking the square root of the sum of squares of the errors associated with various factors, including instrument error. Sauer and Meyer's results for typical measurements are listed in their table 7 on page 19.