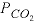of 10
-2.0
atm.This example demonstrates the capabilities of PHREEQC to perform a series of geochemical simulations, with the final simulations relying on results from previous simulations within the same run. The example investigates diagenetic reactions that may occur in zones where seawater mixes with carbonate groundwater. The example is divided into five simulations, labeled part A through part E in table 15.
(A) Carbonate groundwater is defined by equilibrating pure water with calcite at a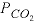
of 10
-2.0
atm.
(B) Seawater is defined by using the major-ion data given in table 9.
(C) The two solutions are mixed together in the proportions 70 percent groundwater and 30 percent seawater.
(D) The mixture is equilibrated with calcite and dolomite.
(E) The mixture is equilibrated with calcite only to investigate the chemical evolution if dolomite precipitation is assumed to be negligible.
The input for part A (table 15) consists of (a) the definition of pure water with SOLUTION input, and (b) the definition of a pure-phase assemblage with EQUILIBRIUM_PHASES input. In the definition of the phases, only a saturation index was given for each phase. Because it was not entered, the amount of each phase defaults to 10.0 mol, which is essentially an unlimited supply for most phases. The batch reaction is implicitly defined to be the equilibration of the first solution defined in this simulation with the first pure-phase assemblage defined in the simulation. (Explicit definition of batch-reaction entities is done with the USE keyword.) The SAVE keyword instructs the program to save the batch-reaction solution composition from the final batch-reaction step as solution number 1. Thus, when the simulation begins, solution number 1 is pure water. After the batch-reaction calculations for the simulation are completed, the batch-reaction solution--water in equilibrium with calcite and CO 2 --is stored as solution 1.
Part B defines the composition of seawater, which is stored as solution number 2. Part C mixes groundwater, (solution 1) with seawater (solution 2) in a closed system in which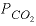 
is calculated, not specified. The MIX keyword is used to define the mixing fractions (approximate mixing volumes) of each solution in the mixture. The SAVE keyword causes the mixture to be saved as solution number 3. The MIX keyword allows the mixing of an unlimited number of solutions in whatever fractions are specified. The fractions (volumes) need not sum to 1.0. If the fractions were 7.0 and 3.0 instead of 0.7 and 0.3, the number of moles of each element in solution 1 (including hydrogen and oxygen) would be multiplied by 7.0, the number of moles of each element in solution 2 would be multiplied by 3.0, and the resulting moles of elements would be added together. The mass of water in the mixture would be approximately 10 kg (7.0 from solution 1 and 3.0 from solution 2) instead of approximately 1 kg when the fractions are 0.7 and 0.3. The concentrations in the mixture would be the same for both sets of mixing fractions because the relative proportions of solution 1 and solution 2 are the same. However, during subsequent reactions it would take 10 times more mole transfer for mixing fractions 7.0 and 3.0 than shown in table 16 because the mass of water would be 10 times greater in that system.
Part D equilibrates the mixture with calcite and dolomite. The USE keyword specifies that solution number 3, which is the mixture from part C, is to be the solution with which the phases will equilibrate. By defining the phase assemblage with “EQUILIBRIUM_PHASES 1”, the phase assemblage replaces the previous assemblage number 1 that was defined in part A. Part E performs a similar calculation to part D, but uses phase assemblage 2, which does not contain dolomite as a reactant.
Selected results from the output for See Mixing are presented in table 16. The groundwater produced by part A is in equilibrium with calcite and has a log 
of -2.0, as specified by the input. The moles of CO
2
in the phase assemblage decreased by about 2.0 mmol, which means that about 2.0 mmol dissolved into solution. Likewise, about 1.7 mmol of calcite dissolved. Part B defined seawater, which is calculated to have slightly greater than atmospheric carbon dioxide (-3.48 compared to about -3.5), and is supersaturated with calcite (saturation index 0.68) and dolomite (2.24). No mole transfers of minerals were allowed for part B. Part C performed the mixing and calculated the equilibrium distribution of species in the mixture, again with no mole transfers of the minerals allowed. The resulting log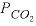 
is -2.20, calcite is undersaturated, and dolomite is supersaturated. The saturation indices indicate that thermodynamically, dolomitization should occur; that is, calcite dissolves and dolomite precipitates. Part D calculates the amounts of calcite and dolomite that should react. To produce equilibrium, 15.61 mmol of calcite should dissolve and 7.853 mmol of dolomite should precipitate. Dolomitization is not observed to occur in present-day mixing zone environments, even though dolomite is the thermodynamically stable phase. The lack of significant dolomitization is due to the slow reaction kinetics of dolomite formation. Therefore, part E simulates what would happen if dolomite does not precipitate; in that case, only a very small amount of calcite dissolves (0.085 mmol) for this mixing ratio.
