National Water-Quality Assessment (NAWQA) Project
Go to:
Adapted from original article published in the Environmental Science &
Technology, v 31, 1997.
Although censored regression has been widely used by statisticians and
economists, it has been rarely used to analyze environmental data
(4). For environmental data, however, the total concentrations
of several contaminants in the environment, each having some censored
observations, may be of interest. This total concentration could be
calculated using a simple summation or a weighted summation, depending
of the interest of the study and compounds being considered. For
example, the potential threats of atrazine contamination to humans and
terrestrial and aquatic ecosystems may depend on total concentrations
of several compounds such as atrazine (ATZ), deethylatrazine (DEA) and
deisopropylatrazine (DIA) in the environment. DEA and DIA can both be
derived from the degradation of ATZ (5). The importance of DEA
and DIA are that they are structurally and toxicological similar to ATZ
(6-8). Therefore, the risks from the same concentration level
of ATZ, DEA, and DIA likely are similar. The actual risk of using
groundwater as a source of drinking water may depend on the total
atrazine-residue concentration (ATZ+DEA+DIA) and not that of ATZ alone.
Therefore, when designing appropriate policies to improve or protect
the groundwater, it is necessary to consider total atrazine residue to
properly determine risk levels. Direct summation of these three
atrazine compounds, however, is not feasible because censored
observations of ATZ, DEA, and DIA are common in groundwater (9).
An appropriate statistical method has been developed to deal with this
issue of censored environmental data.
The purpose of this paper is to present a statistical method developed
for estimating significant factors that affect the total concentrations
of several contaminants from measurements that include censored
observations. The procedure is demonstrated using concentrations of
ATZ, DEA, and DIA in groundwater. The methodology presented in this
paper, however, can be used to analyze similar cases of environmental
contamination involving censored data.
Two groups of ancillary factors
also were collected for each well: hydrogeologic and land use. Because
multicollinearity among the regressors causes inefficiency and
inconsistency, an initial screening procedure implemented in previous
research (13, 14) was used to eliminate variables that have
limited explanatory power. Details of specific factors collected in the
survey are given elsewhere (11, 12). The sample statistics for
selected factors are given in Table 2.
where G indicates the response (dependent) variable,
x is a vector of the explanatory (independent) variables,
g(x) is a function of x, and
represents the modeling error (15). For this study, x is
land use and hydrogeological characteristics, and the response
variable, atrazine residue, G is expressed as
where ATZ, DEA, and DIA are concentration levels of atrazine and two of its
degradation products in groundwater. To estimate significant factors
that affect G in equation (1), it is necessary to estimate values for G
given in equation (2) first. The problem arises because some
observations of ATZ, DEA, and DIA are below the analytical reporting
limit (0.05 µg/L). For levels below the analytical reporting limit, the
observations were recorded as "less than 0.05 µg/L", and their
precise values are unknown.
When a sample is censored, use of a standard estimation procedure such as
simple linear regression by substituting an arbitrary value for censored data
or treating censored data as missing values produces biased and inconsistent
parameter estimates (16, 17). Censored regression analysis provides an
appropriate method to accommodate censoring in the response variable. The
censored regression model is characterized by a latent regression equation
The above likelihood function is for only one compound.
The likelihood function becomes extremely complicated for the case of
three compounds, having 8 possible combinations. The 8 cases are: (1)
ATZ, DEA, and DIA are all observed; (2) ATZ and DEA are observed but
DIA is censored; (3) ATZ and DIA are observed but DEA is censored; (4)
DEA and DIA are observed but ATZ is censored; (5) DIA is observed but
ATZ and DEA are censored; (6) DEA is observed but ATZ and DIA are
censored; (7) ATZ is observed but DEA and DIA are censored; and (8)
ATZ, DEA, and DIA are all censored. For each case, the likelihood
function is a multiplication of either the cumulative density function
or the probability density function of ATZ, DEA, and DIA, depending on
what data is censored. This makes estimation extremely difficult and
is one of the major reasons for estimating the parameters of the
regression equation for each compound separately. Furthermore, ATZ,
DEA, and DIA are log-normally distributed. Therefore, the distribution
of G (sum of ATZ, DEA, and DIA) is unclear. The details of the
likelihood function can be obtained from the authors (because of space
considerations and complexity, it was not provided here).
[An additional alternative approach to deal with the issue we are addressing
here is to incorporate the censoring levels into the sum of the three
compounds. By doing so, the sum of the three compounds is either uncensored
(all three compounds are observed) interval censored (one or two compounds
are censored), or left censored (all three compounds are censored). This
approach, however, oversimplifies the problem for the case of at least one
compound being censored. It is not clear what censoring level should be
used. For example, 0.15 may be used as a censoring level for the case where
all three compounds are censored. But G <0.15 can come from an infinite number
of different combinations (such as ATZ <0.05, DIA <0.05, and DEA <0.05; or
from ATZ <0.10, DIA <0.04, and DEA <0.01). The same issue arises for the case
of either one or two compounds being censored. In contrast, the methodology
proposed in this study provides a precise restriction for each compound when
it is censored. The procedure presented for this study is one that is both
practically and theoretically justified to analyze the type of data used in
this demonstration.]
The procedure just
described can be applied to ATZ, DEA, and DIA to impute the values for
those observations below the analytical reporting limit. With the
estimated dependent variable, atrazine-residue concentrations, the
significant factors that relate to environmental contaminant
concentrations can be found by standard regression procedures.
To identify the
significant factors that relate to atrazine-residue concentrations in
groundwater, an appropriate model selection procedure has to be used.
There is, however, no procedure available for selecting a term in
regression with censored data. LIFEREG and other statistical programs
for analyzing censored data are designed only for estimating the
parameters of a given regression model. They are not programmed to
perform model selection.
To select an
appropriate model with censored regression analysis, the censored
forward regression procedure will be used in this study (21).
The procedure is a forward stepwise procedure used with Tobit model. In
this procedure, variables are added one at a time as long as they
contribute significantly to the fit. The Wald-type statistic is used in
judging whether a new variable should be added to the model. The
significance level is artificially determined as 0.10.
With the selected model for each compound, the
concentration levels for those sites where observations are recorded as
below the analytical reporting limit could be imputed based on equation
(8). The total atrazine-residue concentration for each site can then be
calculated by using observed data for those sites where observations
are above the analytical reporting limit and imputed data for those
below the analytical reporting limit . Finally, the all-subset model
selection procedure (22) can be used to select the final model
for atrazine residue. The adjusted R2 is used for selecting the
final model. Therefore, the all subsets regression procedure simply
picks the model with the highest R2.
With the estimated censored regression equations, the values of censored
observations can be imputed based on equation (8). The values of û
in equation (6) were calculated by
using the estimated parameters from Tables 3-5. The conditional mean
for each compound at each censored site is imputed with equation (8)
also using the estimated parameters from Tables 3-5.
With the estimated mean for each compound (ATZ,
DEA, DIA) at each censored site and a standard deviation, five sets of
observations were generated for each site. With randomly generated
values, the inverse transformation based on equation (8) was used to
obtain an imputed value for each site. At the end of this process, five
pseudo-complete data sets were obtained.
The statistics of the pseudo-complete data are
given in Table 6. The means of the imputed minimum concentrations for
censored data based on the five pseudo-complete data sets were
4.48 x 10-5, 1.274 x 10-4, and 9.576 x 10-9
for ATZ, DEA, and DIA, respectively, much less than the censored
limit of 0.05 µg/L. Previous
research has confirmed the prevalence of ATZ and DEA concentrations in
groundwater below 0.05 µg/L
(24). The frequency of atrazine detection roughly doubles if the
reporting limit is lowered from 0.05 to 0.003 µg/L .
By using the pseudo-complete data, the final model for atrazine residue was
estimated by an all-subset model selection procedure (22),
although other methods, such as the sum of squares analysis, could also
have been used. The final selected models are not given here because of
the issue discussed in the multiple imputation section. The model was
not unique, depending on which pseudo-complete data set is used. In
Table 7, only the sign and significance level for the variables are
given. Five final models selected from five pseudo-complete data sets
for atrazine residue were identical in terms of variables selected,
significant levels, and signs of coefficients indicating the stability
of the model. The model selected estimates based on each
pseudo-complete data set and is the best model obtained from the list
of 20 potential explanatory variables available
(Table 1).
2)Tobin, J. Econometrica 1958, 26, 24-36.
3)Greene, W. H. Econometric Analysis, Macmillan Publishing
Company, New York, NY, 1990.
4)Siymen, D.; Peyster, A.D. Environ. Sci. Technol. 1994,
28, 898-902.
5)Paris, D.F; Lewis, D.L. Resid Rev. 1973, 45,
95-124.
6)Ciba-Geigy Corporation. Summary of Toxicological Data on Atrazine and
Its Chorotrazine Metabolites; Attachment 12, 56 FR 3526,
Ciba-Geigy, 1993.
7)Kaufman, D.D.; Kearney, P.C. Res. Rev.
1970, 32, 235-265.
8)Moreau, C.; Mouvet, C. J.
Environ. Qual. 1997, 26, 416-424.
(9) Kolpin, D.W.; Thurman, E.M.; Goolsby, D.A. Environ.
Sci. Technol. 1996, 30, 335-340.
10) Burkart, M.R.; Kolpin, D.W. J. Environ.
Qual. 1993, 22, 646-656.
(11) Kolpin, D.W.; Burkart, M.R.; Thurman, E.M. Open-File Rep.
U.S. Geol. Surv. 1993, No. 93-114.
12) Kolpin, D.W.; Burkart, M.R.; Thurman,
E.M. U.S. Geol. Surv. Water-Supply Pap. 1994, No. 2413.
13) Liu, S.; Yen, S.T.; Kolpin, D.W.
Kolpin, J. Environ. Qua., 1996, 25, 992-999.
(14) Liu, S.; Yen, S.T.;
Kolpin, D.W. Water Resour. Bull. 1996, 32, 845-853.
(15) Johnston, J. Econometric
Methods, Third Edition, McGraw-Hill Publishing Company, New York, NY,
1984.
(16) Amemiya, T., Advanced Econometrics, Harvard
University Press, Cambridge, MA, 1985.
(17) Liu, S.; Stedinger, J. R. Water Resources Planning
and Management and Urban Water Resources, The American Society of Civil
Engineers, 1991; pp. 27-31.
(18) Miller, D.M.. American Statistician,
1984, 38, 124-126.
(19) Schmee, J.; Hahn, G. J., Technometrics
1979, 21, 417-432.
(20) SAS, Version 6, A Statistical Software System
Registered Trademark of SAS Institute Inc., Cary, North Carolina, USA,
1989.
(21) Lu, J-C; Liu, S; Unal, C. Unal, Department
of Statistics, North Carolina State University, Raleigh, NC, written
communication, 1995.
(22) Draper, N. R.; Smith, H.
Applied Regression Analysis, Second Edition, John Wiley, New York, NY,
1981.
(23) Rubin, D. B.; Schenker, N., J. Am. Stat.
Assoc. 1986, 81, 366-374.
(24) Kolpin, D.W.; Goolsby, D.A.; Thurman, E.M. J.
Envrion. Qual. 1995, 24, 1125-1132.
Jye-Chyi Lu
Dana W. Kolpin
William Q. MeekerABSTRACT
The potential threats to humans and to terrestrial and aquifer
ecosystems from environmental contamination could depend on the sum of
the concentrations of different chemicals. However, direct summation of
environmental data is not generally feasible because it is common for
some chemical concentrations to be recorded as being below the
analytical reporting limit. This creates special problems in the analysis
of the data. A new model selection procedure, named
forward censored regression, is introduced for selecting an appropriate
model for environmental data with censored observations. The procedure
is demonstrated using concentrations of atrazine
(2-chloro-4-ethylamino-6-isopropylamino-s-triazine),
deethylatrazine (DEA, 2-amino-4-chloro-6-isopropylamino-s-triazine),
and deisopropylatrazine (DIA, 2-amino-4-chloro-6-ethylamino-s-triazine)
in groundwater in the Midwestern United States by using the data derived from
a previous study conducted by the U.S. Geological Survey. More than 80% of the
observations for each compound for this study were left censored at
0.05 µg/L. The values for censored observations of atrazine, DEA, and DIA
are imputed with the selected models. The summation of atrazine residue
(atrazine + DEA + DIA) can then be calculated using the combination of
oberved and imputed values to generate a pseudo-complete data set.
The all-subsets regression procedure is applied to the pseudo-complete data
to select the final model for atrazine residue. The methodology presented can
be used to analyze similar cases of environmental contamination involving
censored data.
INTRODUCTION
It is common that some observations of environmental measurements such
as herbicide concentrations in soil, air, and water are recorded as
below specified analytical reporting limits due to measurement
capacities or economical/practical concerns. This practice, however,
creates special problems in the analysis of the data. Statistically, a
data set with observations recorded as being below a certain limit is
called "left censored" or simply "censored". In most environmental
data analyses, censored data implies that values are only reported for
those observations above some predetermined value (1).
When data are censored, censored regression or Tobit regression (2),
is an appropriate method for data analysis (1, 3).
Atrazine Data in Groundwater
The atrazine data used for this statistical
demonstration were collected in a previous study of pesticides in
groundwater of the Midwestern United States by the U.S. Geological
Survey (10-12). A total of 303 wells were sampled for this study
(Fig. 1). During 1991, 589 water samples were collected from these
303 wells in March-April (preplanting) and July-August (postplanting).
The number of samples containing reported concentrations (>0.05 µg/L)
were ATZ (101), DEA (106), and DIA (32), respectively. The maximum ATZ
concentration in groundwaterwas 2.10 µg/L about 30% below the maximum
contamination level (MCL) for atrazine(3 µg/L). The maximum
atrazine-residue concentration, however, was 4.48 µg/L, about 50% above
the atrazine MCL and more than twice the maximum concentration of ATZ alone.
This, however, is not an appropriate procedure for calculating a total
concentration and will be addressed later. The statistical summary for
concentrations above the 0.05 µg/L analytical reporting limit is given
in Table 1.
The Statistical Model
Suppose we are interested in finding the factors that affect the total risk
posed by pesticides in groundwater. The method commonly used to find the
significant factors is regression analysis. Mathematically, this can be
expressed as
![]()
![]()


MULTIPLE IMPUTATION
Although imputing the censored
data at its conditional mean, allowing the use of standard
complete-data methods of analysis, is commonly used in practice; it has
the drawback that it treats the censored data as known values. This
kind of treatment ignores the actual variability in the censored data
values. Research has shown that a multiple imputation with random
sample of size m = 2 can greatly improve the confidence interval
coverage probabilities, performing better than the single sample
imputation method in all studied cases (23). When there are more
data censored, the random sample size should be increased. Comparing
the amount of information missing in the previous study (23) to
the amount of censored data in this demonstration, we selected a random
sample size of 5 to insure a reasonably accurate imputation result.
This method was used to examine the robustness of the parameter
estimation from the pseudo-complete data sets.
EMPIRICAL RESULTS
By using the model selection procedure discussed above, the three censored
regression models for the three atrazine compounds (ATZ, DEA, and DIA) were
selected. The final selected models are given in Table
3 (ATZ)
APPENDIX: Derivation of the Mean if the Truncated Lognormal Distribution
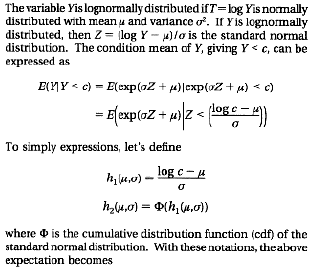
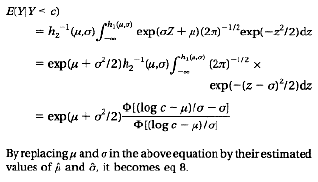
REFERENCES
1)Lawless, J.F. Statistical Models and Methods for Lifetime
Data, John Wiley & Sons, Inc., New York, 1982.
Shiping Liu
BF&S Consulting
Global Business Intelligence Solutions, IBM,
San Francisco, CA
Associate Professor, Department of Statistics
North Carolina State University
Raleigh, NC, 27695
U.S. Geological Survey
400 S. Clinton St.
Iowa City, IA, 52244
(319) 358-3614
Fax: (319) 358-3606
Distinguished Professor, Department of Statistics
Iowa State University
Ames, IA 50011
Next: Tables