Appendix B
Finite Difference Approximations and Boundary Conditions
B1.0 Introduction
As discussed in Section 3.4, the spatial derivatives in the governing
differential equations may be approximated using finite difference
techniques. These techniques are the subject of this appendix. For
a review of finite difference modeling, the reader is referred to
Thomann and Mueller (1987).
We begin the discussion with a brief overview of the finite difference
approximations required for the one-dimensional stream network. This
overview is followed by a development of the equations for the individual
segments or control-volumes that comprise the system. Two concluding
sections discuss a special case of the approximations, boundary
conditions.
B2.0 Finite Difference Equations (FDEs)
Equation (1), the mass balance equation for the stream channel, contains
several spatial derivatives that may be approximated via finite
differences. In general, spatial derivatives and model parameters
need to be defined at both the center of the stream segment and at the
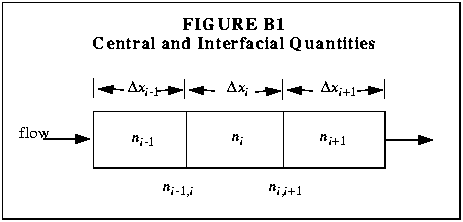
segment's interfaces. These locations are defined in Figure B1,
where an arbitrary quantity, n, is shown. In the figure,
the subscript `i' is used to represent the quantity at the
center of the segment. Quantities at the upstream interface, where
segment i-1 adjoins segment i, are indicated
using the subscript `i-1,i'. In a similar fashion, the
downstream interface is marked using the subscript `i,i+1'.
I. The Center of the Segment
The first task is to evaluate the spatial derivative,
∂n/∂x, at the center of segment i. Using a
centered difference, the spatial derivative of any variable is given
by:
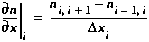 (B1)
(B1)
Note that Equation (B1) introduces the interfacial quantities,
ni-1,i and ni,i+1. Since the
mass balance equations were developed for the center of each segment,
the interfacial quantities should be defined in terms of
ni-1, ni and
ni+1. To do this, we compute the interfacial quantities
by interpolating linearly between the centers of the adjacent
segments. This results in the following definitions:
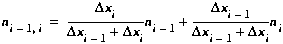 (B2)
(B2)
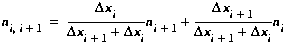 (B3)
(B3)
II. The Segment Interfaces
We must also define the spatial derivatives at the upstream and downstream
interfaces of the segment. These spatial derivative are defined as the
change in n divided by the distance over which the change occurs.
For the upstream interface, this gives:
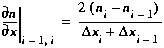 (B4)
(B4)
The same approach is used to evaluate the spatial derivative at the
downstream boundary. This yields:
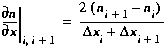 (B5)
(B5)
B3.0 Interior Segments - FDEs
Using the foregoing definitions, it is now possible to approximate the
spatial derivatives in Equation (1). Note that the first term on the
right-hand side of Equation (1) is the `Advection' term
while the second is the `Dispersion' term. These two quantities
are now approximated for the interior segments of the stream network.
Boundary segments, i.e. the first and last segments, represent
special cases that are discussed in Sections B4.0 and B5.0.
I. Advection
Using definition (B1), the advective term may be approximated as:
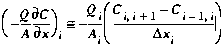 (B6)
(B6)
We now replace the interfacial concentrations (Ci,i+1 and
Ci-1,i) with the definitions given by
Equations (B2) and (B3). This substitution results in a centered
difference approximation for ∂C/∂x,
given equal segment lengths:
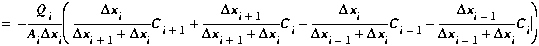 (B7)
(B7)
II. Dispersion
Here again we use definition (B1) to define the spatial derivative:
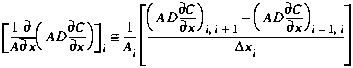 (B8)
(B8)
As the right side of Equation (B8) still contains spatial derivatives,
we need the definitions given as Equations (B4) and (B5). Replacing
the interfacial derivatives, we arrive at:
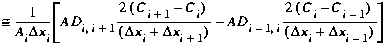 (B9)
(B9)
B4.0 The First Segment - Upstream Boundary Condition
In the previous section, finite difference approximations for the spatial
derivatives were developed. These approximations may be applied directly
to all interior segments in the stream network. A problem arises, however,
when we are dealing with the first segment, as all quantities involving
the subscript i-1 are undefined. Equations (B7) and (B9) must
be modified accordingly.
I. Fixing the Upstream Boundary Condition
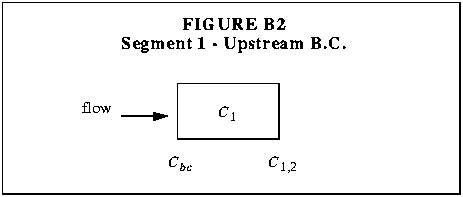
To effectively implement the finite difference equations for the first
segment, an upstream boundary condition must be defined. This condition
is shown in Figure B2, where the interfacial concentration at the
upstream boundary is set to a user-supplied concentration,
Cbc. This quantity is known as the upstream boundary
condition.
II. Advection
Given the definition of Cbc, Equation (B6) can be
modified for use in the first segment:
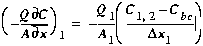 (B10)
(B10)
As with the interior segments, replace the interfacial concentration
(C1,2) using Equation (B3):
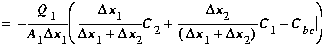 (B11)
(B11)
III. Dispersion
Using the equation developed for the interior segments, the dispersive
term is given by:
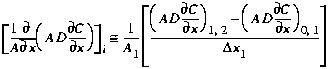 (B12)
(B12)
The first interfacial derivative (at 1,2) is defined as before using
Equation (B5). The second term (at 0,1), requires an additional
equation:
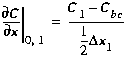 (B13)
(B13)
Note that the forward difference approximation shown above must be used
in lieu of Equation (B4) to avoid introducing C0, the
concentration in the non-existent segment zero. Equations (B5) and (B13)
may now be used:
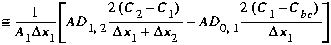 (B14)
(B14)
B5.0 The Last Segment - Downstream Boundary Condition
The finite difference equations developed in Section B3.0 must also be
modified to accommodate the last segment in the stream network. The
required modifications to Equations (B7) and (B9) are shown below.
I. Fixing the Downstream Boundary Condition
Application of Equations (B7) and (B9) to the last segment results in the
introduction of an solute concentration, Ci+1. This
concentration is undefined as segment i+1 does not exist. The
last segment, i, and the fictitious segment, i+1, are
shown in Figure B3.
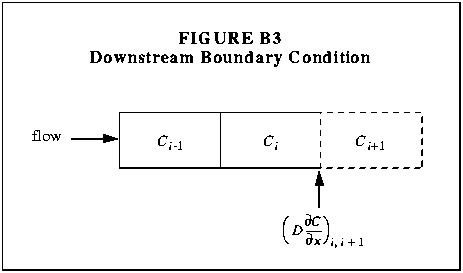
To eliminate Ci+1 from the finite difference
equations, the dispersive flux at the interface between segments
i and i+1 is defined as in Equation (27):
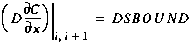 (B15)
(B15)
where DSBOUND is a user-supplied value for the dispersive flux. Note that if
DSBOUND is set equal to zero, Equation (B15) is a zero gradient
boundary condition (Arden and Astill, 1970).
Using the definition of the interfacial first derivative given by
Equation (B5), Equation (B15) is solved for Ci+1,
yielding:
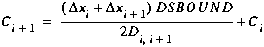 (B16)
(B16)
Equation (B16) is now used to eliminate Ci+1 from
Equations (B7) and (B9).
II. Advection
Substituting Equation (B16) into (B7) and replacing
 xi+1 with
xi+1 with
 xi, we arrive at the finite difference
approximation of the advection term:
xi, we arrive at the finite difference
approximation of the advection term:
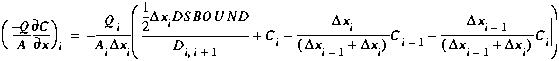 (B17)
(B17)
III. Dispersion
The finite difference approximation of the dispersion term is now
developed by substituting Equation (B16) into (B9) and replacing
 xi+1 with
xi+1 with
 xi:
xi:
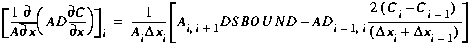 (B18)
(B18)


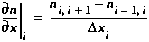 (B1)
(B1)
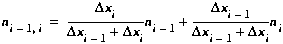 (B2)
(B2)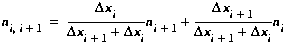 (B3)
(B3)
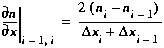 (B4)
(B4)
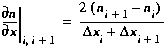 (B5)
(B5)
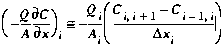 (B6)
(B6)
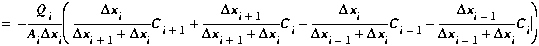 (B7)
(B7)
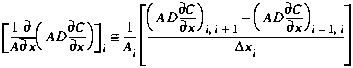 (B8)
(B8)
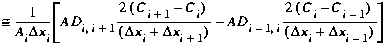 (B9)
(B9)

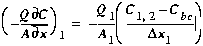 (B10)
(B10)
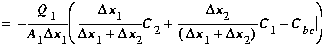 (B11)
(B11)
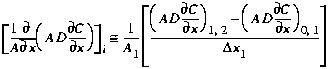 (B12)
(B12)
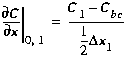 (B13)
(B13)
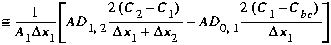 (B14)
(B14)

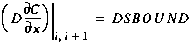 (B15)
(B15)
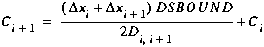 (B16)
(B16)
 xi+1 with
xi+1 with
 xi, we arrive at the finite difference
approximation of the advection term:
xi, we arrive at the finite difference
approximation of the advection term: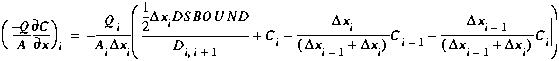 (B17)
(B17)
 xi+1 with
xi+1 with
 xi:
xi: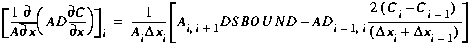 (B18)
(B18)