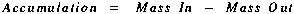 (A1)
(A1)
Mechanistic models such as the one presented in this report are based on a fundamental engineering principle, conservation of mass. This principle states that for a finite volume of water, mass is neither created or destroyed (see Chapra and Reckhow, 1983). In short, mass conservation implies that:
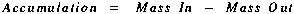 (A1)
(A1)
Equation (A1) is often called a mass balance equation. This mass balance
must be applied to a finite volume of water, known as a control volume.
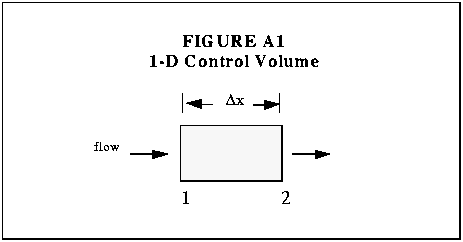
A control volume for our one-dimensional system is shown below. Note that
the terms 'segment' (introduced in Section 3.2) and 'control volume' can
be used interchangeably. In figure A1,
 x
represents the segment length, while `1' and `2' are used to demarcate
the upstream and downstream boundaries of the control-volume.
x
represents the segment length, while `1' and `2' are used to demarcate
the upstream and downstream boundaries of the control-volume.
The remainder of this appendix is devoted to the formulation of differential equations based on Equation (A1). To accomplish this task, we first define `Accumulation' and then proceed to develop the `in' and `out' terms for each process given in Table 1. This procedure is carried out for both the stream channel and the storage zone.
 (A2)
(A2)
where
We can now expand Equation (A2) using the chain rule, yielding:
C in-stream solute concentration [M/L3] V volume of the main channel segment [L3] t time [T]
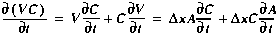 (A3)
(A3)
where
x
segment length [L] A stream cross-sectional area [L2]
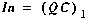 (A4)
(A4)
where Q is the volumetric flowrate [L3/T].
Next, the mass advected out of the control volume, i.e. across the downstream boundary, is given by:
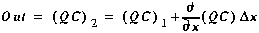 (A5)
(A5)
Finally, we combine the `In' and `Out' terms, giving:
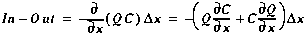 (A6)
(A6)
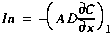 (A7)
(A7)
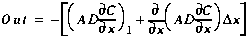 (A8)
(A8)
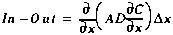 (A9)
(A9)
where D is the dispersion coefficient [L2/T].
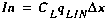 (A10)
(A10)
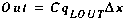 (A11)
(A11)
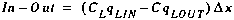 (A12)
(A12)
where
CL solute concentration of the lateral inflow [M/L3] qLIN lateral inflow rate [L3/T-L] qLOUT lateral outflow rate [L3/T-L]
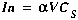 (A13)
(A13)
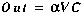 (A14)
(A14)
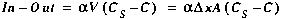 (A15)
(A15)
where
Note that the exchange coefficient,
storage zone exchange coefficient [/T] CS storage zone solute concentration [M/L3]
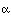 , is defined as the fraction of the main channel volume
that is exchanged with the storage zone, per unit time.
, is defined as the fraction of the main channel volume
that is exchanged with the storage zone, per unit time.
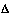 x gives:
x gives:
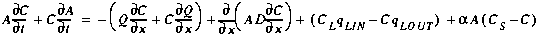 (A16)
(A16)
Although Equation (A16) represents a mass balance for a one-dimensional stream, it may be simplified using the water balance shown below.
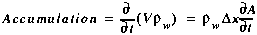 (A17)
(A17)
where 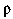 w is the
density of water [M/L3].
w is the
density of water [M/L3].
The inflow term for the water balance is the sum of the water advected across the upstream interface and the water entering via lateral inflow:
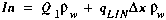 (A18)
(A18)
Similarly, outflow is the sum of the water advected out and that leaving through lateral outflow:
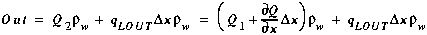 (A19)
(A19)
Finally, the water balance is completed by combining Equation (A17)
through (A19), and dividing by
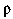 w
w
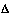 x:
x:
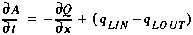 (A20)
(A20)
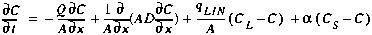 (A21)
(A21)
This equation is presented in Section 3.2.1 as Equation (1).
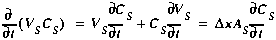 (A22)
(A22)
where
Note that the storage zone area, AS, is assumed to be constant in time.
VS volume of the storage zone segment [L3] AS storage zone cross-sectional area [L2]
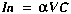 (A23)
(A23)
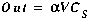 (A24)
(A24)
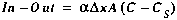 (A25)
(A25)
where 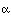 is the
fraction of the main channel volume that is exchanged with the storage
zone, per unit time.
is the
fraction of the main channel volume that is exchanged with the storage
zone, per unit time.
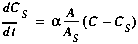 (A26)
(A26)
This governing equation is presented in Section 3.2.1 as Equation (2).